Identifying Users

The ultimate objective of online tracking is to identify the user who is accessing a website. If a user can be uniquely identified, then their interactions and behaviors while on the website can be associated with a real person. When websites use common tracking technologies provided by third parties, users can be tracked across websites. If a user profile is associated with a browser on another device, or with an application on a mobile phone, the user can be identified and tracked across any and all devices they use. Some users will attempt to limit this tracking, but companies can utilize covert techniques to try to identify even an uncooperative user.

Video Lecture

Overt and Covert Identification

Users can be identified online voluntarily or involuntarily. With overt identification, the user either knows or reasonably should know that they are being identified (and tracked). On the other hand, covert identification techniques try to identify users without first obtaining each user’s informed consent (meaning that the user knows or reasonably should know they will be identified and tracked, and they explicitly agree to be identified and/or tracked).

Overt identification is normally implemented by having a user register for a website or service using some kind of unique identifier, such as an email address or telephone number. The user is then either required or encouraged to sign in to the site and remain signed in. Large companies that employ these techniques include Alphabet (Google), Meta (Facebook), and Netflix. Although most users of these services do not bother to read and understand the terms of service and privacy policies, they are giving informed consent to overt identification. Informed consent exists because a person could reasonably be expected to read and understand the companies’ published policies before clicking the “accept” or “agree” button. Since the user agrees to these terms when creating accounts on each service, user identification is overt.

Unfortunately, the “opt-out” attitude toward privacy invasion means that companies also routinely utilize covert methods to identify users. Covert identification uses computational techniques to measure properties of a browser or device to generate a unique identifier. Covert identification is more concerning than overt identification, since the user does not normally have informed consent that they will be tracked in this way. While most websites have a privacy policy and contain service terms, there is little valid justification for a reasonable person to read these documents if they have no intent of creating an account or otherwise entering into a voluntary business relationship with the website operator.

Countermeasures to Overt Identification

Maintaining privacy against overt identification seems simple enough: just don’t sign into a website if there is no need to do so, and sign out of websites when finished using them. In practice, this approach does not tend to work well. Websites that employ overt identification methods may also be using covert techniques to track users that are not currently signed into the site. Covert and overt identification methods can be combined to link the unique identifier created by covert tracking to the user’s overtly provided personal information.

Sites employ both overt and covert methods for simple economic reasons. Many of the services provided by these companies are “free” to the user, meaning they are offered at zero monetary cost. Other services charge a fee but either charge below their actual costs or look for additional means for boosting profits. Running a site or service always costs money: servers aren’t free, Internet access represents an ongoing cost, system administrators and other staff have to be paid, and so forth. How is it then possible for a website to offer a service to a large number of people without charging money in exchange?

The answer is that these websites do charge the user, but the currency is not money. Instead, these companies trade in the currency of personal information. As users interact with the service, comprehensive profiles are built, which are then sold to advertisers and/or data brokers to pay for the real monetary costs of providing the website. Users who sign out of these services could be bad for profits if they become difficult to track.

Covert identification techniques work to mitigate the problem (from the company’s perspective) of users who will utilize a “free” service but limit the amount of personal information they are willing pay in return. A typical approach is to assign a unique identifier to each browser or device that connects to the service in any way. If that user later signs into the service overtly with the same browser on the same system, information collected covertly can be added to the known user’s profile. When tracking can be done across devices and websites, behavioral information is eventually tied to an identifiable person whenever they sign into that service on any linked device. The key to this technique is to be able to generate the unique identifier before the user signs in (or signs up) from an unknown browser or device. Understanding how this identifier can be generated requires a little bit of information theory.

Information Entropy

Claude Shannon (Figure 1) is regarded as the founder of the field of information theory. Born in 1916, Shannon earned his Bachelor of Science degree at the University of Michigan before completing a master’s and doctorate at MIT. While he was still a graduate student, Shannon was the first known person to apply Boolean algebra to circuit design, revolutionizing the development of electronics (and eventually, computers). During his working career at Bell Labs (and later as an MIT professor), Shannon developed a number of useful theories that were initially applied to communications circuits but were later adapted to other applications.¹

Some of Shannon’s initial work that forms the basis of information theory concerns the concept of information entropy, which he published in serial form in a series of technical reports at Bell Labs.^3,4 In simple and practical terms, information entropy is a measure of the differences between two things based on certain amounts of randomness. This randomness comes from different ways data are processed, differences in the machines doing the processing, different communications technologies, and so forth. Randomness is measured in units of bits. A bit represents the state of a digital switch: it is either off (0) or on (1). These two values (0 and 1) are the two valid digits in the binary, or base two, number system. The word “bit” is actually a shortened form of “binary digit”.

A unique identifier can be created by concatenating these bits of information entropy into a larger binary number (base two). If a sufficient amount of entropy can be collected from a user’s browser or device, the number of bits in the identifier increases. Whenever enough bits of entropy can be collected to identify a single browser or device among the billions of others on the Internet, a practical covert user identification system can be implemented.

Bits of Information

To determine how many bits of information is “enough” to identify a device, we only need to figure out how big the binary number needs to be in order for each device to be given a unique value. To simplify this concept, let’s assume that each individual human user has only one device. Once we have identified this browser or device, we will have identified its user.

Understanding the mathematics behind information entropy first requires figuring out how many unique identifiers can be made from a given number of bits. Let’s start with a single bit. A single bit can have one of two values: 0 or 1. Since we have two different values (namely, 0 and 1), we can create two different unique identifiers. One of these identifiers is the number 0, while the other is the number 1. If we only had to distinguish between two users, we could assign one of the users the “0” label and give the other user the “1” identifier.

If instead we have 2 bits, we can list out all the identifiers we could make by setting each bit to 0 or 1 in combination. Writing out all the possibilities yields:

• 00
• 01
• 10
• 11

Counting the above list shows that 2 bits can provide 4 unique identifiers, which is the double the number of identifiers achievable with only 1 bit. What happens if we add a 3rd bit? All the combinations would be:

• 000
• 001
• 010
• 011
• 100
• 101
• 110
• 111

Counting the number of items in the above list tells us that we have 8 unique identifiers available with 3 bits of entropy. We therefore doubled the number of available identifiers again by adding a single bit. Let’s see if this trend continues by adding 4th bit:

• 0000
• 0001
• 0010
• 0011
• 0100
• 0101
• 0110
• 0111
• 1000
• 1001
• 1010
• 1011
• 1100
• 1101
• 1110
• 1111

When we count the items in this list, we see that we have 16 unique identifiers, confirming that adding 1 bit doubled the number of identifiers once again. This looks like a pattern: 1 bit provides 2 identifiers; 2 bits provide 4 identifiers; 3 bits provide 8 identifiers; and 4 bits provide 16 identifiers. We therefore expect that 5 bits would provide double the number of identifiers as 4 bits, or 32 identifiers in total.

Number of Identifiers

Now suppose that we have 12 bits of entropy available. It would be possible to work out how many identifiers we would have by starting from the 5-bit calculation we’ve already done and doubling once for each bit. However, there is a shorter way to perform this calculation. We just need to find a formula that describes the number of unique identifiers as a function of the number of bits of entropy. That’s a lot to write, so let’s use a capital N to represent the number of unique identifiers. In computing, we normally use a lowercase b to represent the word “bits” (an uppercase B is used for bytes, which are units of 8 bits). Since each increase in b doubles N, the relationship can be described mathematically as shown in Formula 1:

To obtain N for b = 12, we can use a scientific calculator that has an exponent button. On the calculator shown in Figure 2, the exponent button is labeled x^y. The calculation 2¹² is performed by pressing 2, then x^y, then 12, then =. Most other scientific or graphing calculators will have a similar button.

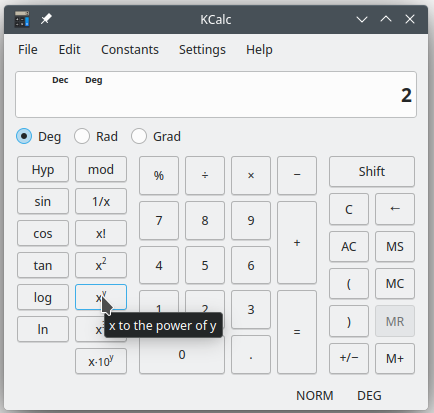
Using the calculator, we can compute N = 2¹² = 4,096. Therefore, 12 bits of entropy can provide 4,096 unique identifiers.

Number of Bits

Someone engaged in covert surveillance might be more interested in knowing how many bits of entropy need to be collected in order to identify a user to a certain level of uniqueness. In this case, we know the number of unique identifiers needed but not the number of bits. In terms of Formula 1, we know N but need to solve the equation for b.

To undo an exponent, we need to use another mathematical function called a logarithm. Specifically, we have to use a base 2 logarithm to undo the exponent on the right side of Formula 1, since the base is 2 and the exponent is b. The base 2 logarithm in math is written as log₂, with the subscript 2 indicating the base.

Recall that we can do almost anything to an equation in mathematics as long as we do the same thing to both sides of the = sign. If we take the base 2 logarithm of both sides of Formula 1, we get the equation shown in Formula 2:

Now the whole point of using a logarithm is to undo an exponent. In our case, the base 2 logarithm undoes an exponent with a base of 2. Formula 3 shows what happens when we perform this step:

Remember that we can write a mathematical equation backwards and still have the same equation. Therefore, Formula 3 is equivalent to the following Formula 4:

Formula 4 is more convenient to use for our purpose here. It will give us the number of bits of entropy we need to be able to produce the number of unique identifiers we want. There is only one small problem with this formula: our scientific calculator doesn’t have a log₂ button. It has a “log” button, which computes a base 10 logarithm. It also has an “ln” button, which computes the natural logarithm (log_e, where e is approximately 2.71828182846), but we’ll ignore that button.

Fortunately, there is a property of logarithms that will allow us to change bases. This property is expressed in Formula 5:

Since our “log” button on the calculator takes a base 10 logarithm, and we want a base 2 logarithm, we substitute 2 for x and 10 for z in Formula 5. If we replace y with N, we get Formula 6:

The base 10 logarithm of 2 can be calculated by typing 2 into the calculator and pressing the “log” button. This value is about 0.30103. Therefore, we can rewrite Formula 4 as shown in Formula 7:

To test that Formula 7 is correct, let’s undo what we know from the previous section. We computed that 12 bits of entropy gives us 4,096 unique identifiers. If we type 4096 into our calculator, press the log button, then divide that by 0.30103, we get a result of 11.9-and-change. However, remember that a bit only has two states: it is either on or off, 1 or 0. Therefore, if we get a partial number of bits in this calculation, we always need to round up to the next whole number of bits. Rounding our result up to the next whole number gives us 12, which is the result that we expected.

As a side note, some theoretical work involving information entropy does present fractional numbers of bits. While fractional bits aren’t possible inside real computers, they allow us to avoid overestimating the amount of entropy that can be measured from two different processes. For example, if we know that one set of properties inside a Web browser provides 6.3 bits of entropy, while another provides 5.2 bits, we would add 6.3 + 5.2 = 11.5 and then round up to 12. If we rounded up first, we would add 7 + 6 = 13, and the resulting total entropy would be overstated by one bit.

Examples

As of the February 6, 2023 US Census population clock⁵ at an arbitrary time of day, there were an estimated 334,354,549 people in the United States and 7,950,063,340 people on Earth. How many bits of information do we need to identify every person in the country? What about every person on the planet?

Let’s start with the United States, with a population of 334,354,549. Applying Formula 7, we substitute 334354549 for N. Typing in that number and pressing the log button on our calculator gives a value of about 8.52421. Dividing 8.52421 by 0.30103, then rounding up to the next whole number, gives us a value of 29. We therefore need 29 bits of entropy to be able to assign a unique identifier to every person in the United States.

The world population of 7,950,063,340 is much bigger, so surely we’ll need a lot more bits, right? To find out, substitute 7950063340 for N in Formula 7. Type that into the calculator, then hit the log button to get about 9.90037. Divide that number of 0.30103, then round up to the next whole number, which is 33. Therefore, 33 bits of entropy are enough to assign a unique identifier to every person on planet Earth!

Notice that the properties of exponents and logarithms mean that we only need 5 extra bits to go from identifying each person in the United States to identifying everyone in the world. The scarier thing about this result is that 33 bits of entropy isn’t that many in modern Web browsers.

Sources of Entropy

Web browsers produce a considerable amount of entropy. First, there is the choice of browser itself (for example, is the user using Firefox or Chrome). Then, each browser has a unique version number, which it provides to websites via the User-Agent header⁶. Various different versions of browsers are running on different operating systems (Linux, macOS, Windows, FreeBSD, etc.), and the operating systems have different versions. Browser configurations, installed fonts, available plugins, and other properties vary from browser to browser, since users tend to install different things and tweak different settings. Prior to the addition of the HTML 5 canvas element, browsers were found to provide 18 to 19 bits of entropy.⁷ The HTML 5 canvas element adds between 5 and 6 bits of entropy on top of that.⁸ Therefore, without any countermeasures, a modern browser can reasonably be expected to give away at least 23 bits of entropy. Remember that we only need 10 more bits to identify every person on Earth! Browsers are, in general, privacy dumpster fires.

The reason for this state of affairs is that humankind’s quest to make fancier and more dynamic websites has introduced features into browsers that make them give away a lot of information and are harmful to user privacy. There are really only 3 major browser engines in existence as of 2023 (Blink, which powers Google Chrome and Microsoft Edge; Gecko, which powers Firefox; and WebKit, which power’s Safari), and all 3 of them implement these harmful standards. Therefore, Web designers can build sites on the assumption that all these features are available, effectively creating a dependency on them. Without these features enabled, many sites simply will not work.

Harmful technologies that all major browsers support include:

1. The Document Object Model (DOM)
2. JavaScript
3. The HTML5 Canvas element (especially when combined with JavaScript)
4. Cookies
5. WebAssembly

Fortunately, privacy researchers are working on browser-related issues and have developed tools to measure the entropy provided by each browser.⁹ HTML5 has rendered most browser plugins obsolete, removing one major historical source of entropy. However, one potential area for concern is looming on the horizon in the form of WebAssembly, which is being developed as a partial replacement for JavaScript.¹⁰ WebAssembly has the potential to be a privacy and security nightmare, since it will permit easier obfuscation of website code.¹¹ Obfuscated code could be more difficult to analyze and block, allowing trackers, cryptominers, and various kinds of malware to run inside the browser.

References and Further Reading

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.