IEEE 754 Standard
In the previous lesson, we saw that it is possible to approximate real numbers using fixed-sized floating-point values. Central Processing Unit (CPU) cores generally operate using integer arithmetic, so extra hardware is needed, in the form of Floating-Point Units (FPUs), to perform floating-point computations quickly. In order to be able to design consistent hardware that produces the same result each time a calculation is performed, it is necessary to adopt some standards that any manufacturer can follow. The IEEE 754 standard for floating-point arithmetic provides these necessary guidelines.
Video Lecture
Standardization
At a fundamental level, recall that computers are just giant collections of digital switches. With a little design work, we could make up our own format for storing floating-point numbers. Code written for our computer with our custom floating-point representation would work fine as long as we didn’t have any implementation errors. However, if we wanted to run our code on someone else’s computer, or if they wanted to run their code on ours, problems would quickly arise unless we both happened to choose exactly the same representation for floating-point values.
A solution to this interoperability problem is for everyone to implement floating-point numbers in the same way. This approach, called standardization, ensures that software is easily moved from one system to another. Furthermore, standards ensure that computers that communicate over a network will see the name numbers at each end of the communications channel. They also provide means to test that the same computation produces the same result every time.
For floating-point representations inside computer systems, the prevailing standard as of late 2020 is the IEEE 754-2019 standard.1 This standard is published by the Institute of Electrical and Electronics Engineers (IEEE) and is developed and revised by committees of scientists and engineers with expertise in the field. There are quite a few details in the standard, including rules for representation of floating-point numbers using both binary and decimal bases, rounding rules, standard operations, and exceptions (errors). In this lesson, we’re only going to look at the basics of IEEE 754, since the details are abstracted away for us at the IT level.
Review of Scientific Notation
The basic premise behind storing floating-point numbers with varying levels of precision, while providing for an adequate range between minimum and maximum values, is based on the idea of storing two numbers. The first number expresses the digits of the value we want to represent, while the second number contains the magnitude by which we scale the first number to get the final number. You have likely seen a similar system in use with decimal numbers: scientific notation.
Scientific notation allows us to write really large numbers conveniently. Consider these two equivalent representations for the quantity of 1 mole:
602214076000000000000000
6.022 * 1023
Two things are different with these two representations. The first representation contains more significant figures, meaning that there are more digits before the trailing zeros begin. As a result, the first representation has more precision.
The second difference arises with the notation that is used. In the first representation, the number is extremely long (24 digits) and would be cumbersome and error-prone to write each time it is needed. Conversely, the second representation uses scientific notation: it abbreviates the significant digits to an acceptable level for most computations, then it replaces the trailing zeros by the equivalent power of 10. It would be numerically equivalent to write:
6022 * 1020
However, the convention for scientific notation only permits one digit to the left of the decimal point, so we write 6.022 * 1023 instead. Since the scientific consensus, or the standard representation, follows the same rules for scientific notation, a scientist can quickly see that 6.022 * 1023 refers to a mole. Moreover, a scientist can also quickly recognize a number based upon its magnitude: 6 * 1023 is close to a mole, while 3 * 1023 is about half a mole. Standardization makes such quick identifications possible.
Encoding
IEEE 754 notation uses a similar concept as that used in scientific notation, except that binary numbers are usually used inside computer systems, and we have the usual accuracy and precision constraints that come with floating-point representations of real numbers. In IEEE 754, the first bit of the number is the sign bit, which indicates whether the rest of the number is positive or negative. Following the sign bit is a biased exponent field, which works somewhat like the exponent on the 10 in scientific notation. After the biased exponent field comes the trailing significand field, which stores the value that would be multiplied by the base raised to the exponent (some power of two in this case) to get the result in standard notation. Figure 1 illustrates the basic layout of an IEEE 754 floating-point number.
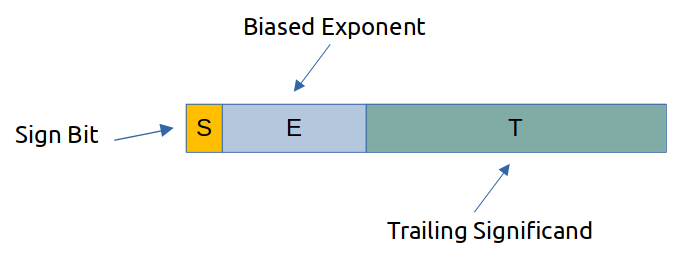
The IEEE 754 representation is a signed magnitude representation, so the value of the number is first calculated before considering the sign bit. If the sign bit is 1, the value is negative; if zero, the value is positive. As a consequence, there are two representations for the number zero: -0 and +0.
There are also some other special values that can be represented if the biased exponent field (E) has all its bits set to 1. When this occurs, the value of the trailing significand (T) determines which special value is represented. If T=0, then the value represents infinity (+∞ if the sign bit is 0, -∞ if the sign bit is 1). If T≠0, then the special value NaN is represented. NaN, which stands for Not a Number, may be used as the result of an invalid computation. Some software applications handling data may also use NaN to represent missing data or a number field that does not yet have a value.
For any other value of the biased exponent field (E), a regular number is represented. If E is at least 1, the number is a normal number, while E=0 indicates a subnormal number whenever the trailing significand (T) field is not zero. If both E and T are zero, then the number 0 is represented in either its positive (sign bit 0) or negative (sign bit 1) form.
Normal numbers are represented with biased exponents. In simple terms, the exponent field is divided roughly in half by subtracting a bias value. If the biased exponent field represents a number greater than the biased value, a positive exponent is applied, allowing large numbers to be represented. On the other hand, a value less than the bias value in the biased exponent field allows for the representation of small numbers (those with negative exponents).
When numbers are extremely close to 0 (but not exactly 0), there is a point at which a normal representation with floating-point will round the value to 0. IEEE 754 delays the point at which this happens by providing for subnormal numbers. Whenever the biased exponent is zero, and the trailing significand is not zero, a subnormal number is represented. Some precision is lost in this representation, and there is a finite limit to the number of bits available, so subnormal numbers only delay rounding to zero as numbers approach zero: they do not prevent the rounding from happening if the magnitude becomes small enough.
Precision
The IEEE 754 standard defines various levels of precision that can be used to store floating-point numbers. As the desired level of precision increases, the storage size (in bits) increases. In addition, the minimum and maximum values that can be represented, before jumping to +/-∞, increase with the precision level. Table 1 lists three standard levels of precision using 32, 64, and 128 bits. Software developers and programmers normally refer to these levels of precision as single, double, and quad.
| Type | Bits | Sign Bits | Biased Exponent Bits | Trailing Significand Bits |
|---|---|---|---|---|
| Single Precision | 32 | 1 | 8 | 23 |
| Double Precision | 64 | 1 | 11 | 52 |
| Quad Precision | 128 | 1 | 15 | 112 |
For any level of precision, there is only one sign bit. However, higher levels of precision provide for significantly more trailing significand bits, increasing the accuracy of a floating-point representation of a real number. The biased exponent bits increase modestly with increasing precision, as even a single precision number can represent values up to about 3.4 * 1038.
Exceptions
Whenever an invalid operation occurs involving IEEE 754 floating-point numbers, the specification provides for an exception to be raised by the computer hardware. An exception permits the computer’s operating system to pass an error indication to the program that caused the exception, notifying the program that the result of the calculation is invalid.
Hardware Implementations
Central Processing Unit (CPU) cores on computers natively work using integer arithmetic. If the system needs to support floating-point arithmetic, there are two options: write software to perform the computation using a sequence of steps on the processor (soft float), or add special circuitry to the computer to handle the computations in hardware (hard float). Hard float circuitry in modern desktop computers is implemented by the floating-point unit (FPU) that is found inside many modern CPUs. Back in ancient times (such as the 1980s), hardware floating-point support had to be added by purchasing and installing a math coprocessor (Figure 2) chip.

It is still possible to find embedded CPUs and microcontrollers that do not have floating-point units. For some applications, integer arithmetic is sufficient, and leaving out the FPU reduces both initial cost and energy consumption. Similar cost reductions sometimes are used in desktop and server CPUs, where the number of integer cores can exceed the number of available floating-point units. For example, the AMD Magny-Cours series of CPUs from 2010 contained 2 integer cores sharing a single FPU.3 As a result, software applications that required floating-point arithmetic effectively only had half the cores available when compared to applications using only integer arithmetic.
Finally, we must observe that adherence to a standard is critical for hardware FPU implementations. Without a standard like IEEE 754, each computer system would need custom hardware to perform floating-point arithmetic using the custom representation the designers chose for that system. Since the custom representation would also require custom software, the cost of the entire computer system would be significantly higher without standardization. For this reason, the IEEE 754 standard is widely adopted, and the vast majority of CPUs with hard float capabilities will use IEEE 754 representations for floating-point numbers.
Notes and References
-
IEEE. IEEE Standard 754-2019. July 22, 2019. (CCU students: access the standard via IEEE Xplore through the Kimbel Library website.) ↩
-
Image Credit: Bumper12 (via Wikimedia Commons). License: Public Domain. ↩
-
Advanced Micro Devices. AMD Opteron 6200 Series Processors Linux Tuning Guide. 2012. ↩
