Number Bases
So far, we’ve seen how to count on our human fingers, how to extend the count to cool robot hands with 15 fingers each, and how to restrict the count to cheap robot hands with only 1 finger each. Our robotic design was based on a human concept of hands, of which we have two. But who says we can only put 2 hands on our robot? What if we put an arbitrary number of hands on our robot, with an arbitrary number of fingers per hand?
Video Lecture
Counting with 3 Cheap Robot Hands
What happens if we give a robot 3 or 4 cheap hands? Or 8 cheap hands? Since we only use a single character inside the parentheses in our shorthand notation, it’s easy to extend the notation to support extra hands. We’ll begin by counting with 3 cheap robot hands (Table 1).
| Hand 1 Finger | Hand 2 Finger | Hand 3 Finger | Shorthand | Value |
|---|---|---|---|---|
| down | down | down | (000)2 | 0 |
| down | down | up | (001)2 | 1 |
| down | up | down | (010)2 | 2 |
| down | up | up | (011)2 | 3 |
| up | down | down | (100)2 | 4 |
| up | down | up | (101)2 | 5 |
| up | up | down | (110)2 | 6 |
| up | up | up | (111)2 | 7 |
With 3 robot hands, perhaps attached to 3 different arms, we can count as high as 7. We can see from the table above that (111)2 is equal to 7 in our familiar base 10 notation. Previously, we established that the rightmost number counts ones, corresponding to the number of fingers raised on the right hand. We also established that the number to the left of the rightmost number counts the number of fingers raised on the second hand, the value of which is obtained by multiplying by the subscript. But what happens with the 3rd hand?
Looking back at Table 1, the added leftmost hand does not do anything until we count above 3. Counting 0, 1, 2, and 3 works the same way as it did when we only had 2 cheap robot hands. When we raise the finger on the newly added hand, then lower the others, we count the value 4. But how is the value 4 related to the subscript 2? There are a few possibilities here, since 2 + 2 = 4, 2 * 2 = 4, and 22 = 4. Let’s see how high we can count if add more hands, and look for a pattern.
Adding More Hands
Table 2 lists the highest values we can count with 1 to 8 of our cheap robot hands. Notice that I put a space in between groups of 4 cheap robot hands once we’re over 4 total hands. Writing (1111 1111)2 makes it easier to read the total number of hands than writing (11111111)2. This convention is purely to improve readability, and the space does not change the underlying meaning.
| Cheap Robot Hands | All Fingers Extended | Maximum Counted Value |
|---|---|---|
| 1 | (1)2 | 1 |
| 2 | (11)2 | 3 |
| 3 | (111)2 | 7 |
| 4 | (1111)2 | 15 |
| 5 | (1 1111)2 | 31 |
| 6 | (11 1111)2 | 63 |
| 7 | (111 1111)2 | 127 |
| 8 | (1111 1111)2 | 255 |
With only 1 cheap robot hand, we can only count to 1, and the subscript does not matter. We already know what happens with 2 cheap hands: the left number is multiplied by the subscript (2). With 3 cheap robot hands, we can count to 7, and the leftmost hand represents 4, as we saw in Table 1. At 4 cheap robot hands, we can count to 15. Notice how we’re building up each time we add a hand? With 1 hand, we could only count to 1. Adding a second hand let us count to 3, with the value of the second hand equal to 2 (and 2 + 1 = 3, right?). When we added the third hand, we could count to 7, which is 4 + 3, and the leftmost hand was worth 4. Continuing this pattern, adding the 4th hand gives us 15, and 15 - 7 is 8.
Adding the 5th hand lets us count to 31, and 31 - 15 = 16. Similarly, adding the 6th hand allows us to count to 63, and 63 - 31 = 32. When the 7th hand is added, we can count to 127, and 127 - 63 = 64. Finally, adding the 8th hand lets us count up to 255, and 255 - 127 = 128. The pattern is the differences is 1, 2, 4, 8, 16, 32, 64, 128.
Notice in the pattern that each additional hand doubles the value of the highest hand before it. So what we have here is an exponential relationship. If we write the maximum values of each hand from highest value to lowest, we get:
27, 26, 25, 24, 23, 22, 21, 2^0
To get the biggest value we can represent with 8 cheap robot hands, we just need to add these numbers together:
27 + 26 + 25 + 24 + 23 + 22 + 21 + 20 =
128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
Relationship of Cool and Cheap Robot Hands
Take a look at how high we can count with 4 cheap robot hands in Table 2. We can count to 15, which is the same value we could count with a single cool robot hand (the one with 15 fingers). With 8 robot hands, we can count to 255, which is what we could do with 2 of the cool robot hands. It turns out that for any number of robot hands (cool or cheap), we can substitute 4 cheap robot hands for 1 cool robot hand. So if we have 2 cool robot hands, we can substitute 8 cheap ones and still be able to count to the same value.
Why do we care? Well, remember that to build two cool robot hands, we need 30 springs, 30 electromagnetic coils, and 60 wires. We can build 8 cheap robot hands using 8 springs, 8 electromagnetic coils, and 16 wires. This approach would be less expensive, yet it would let us count just as high as we could with the more expensive cool robot hands.
Moreover, with cheap robot hands, we can activate the electromagnet on each hand with a simple switch. If we turn the switch on, power flows through the electromagnet and extends the finger. Turning the switch off cuts power to the electromagnet, the spring retracts the finger.
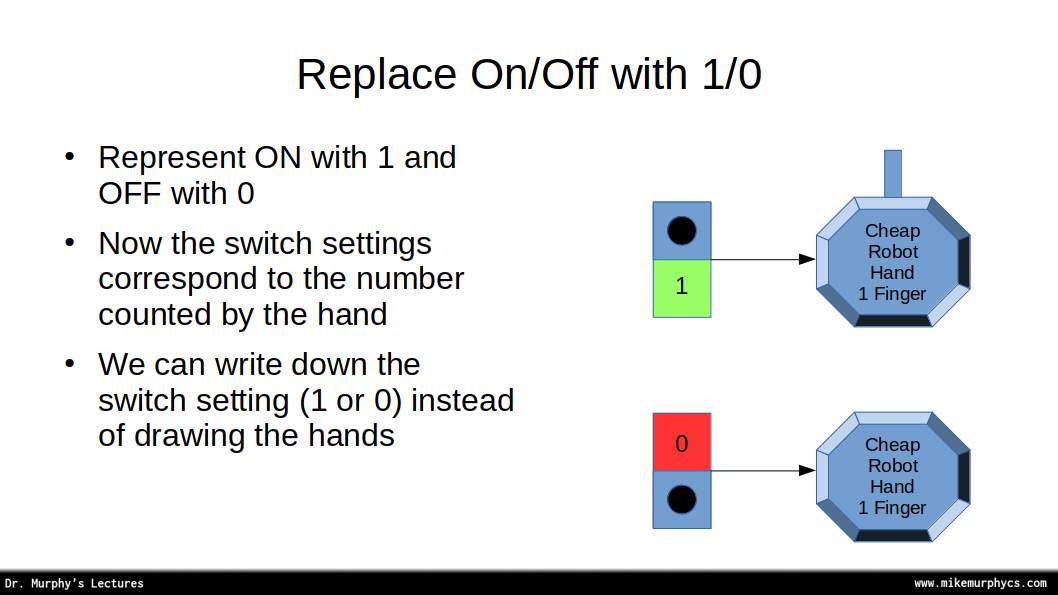
Figure 1: Controlling the finger on a cheap robot hand using a switch labeled 0 (off) and 1 (on).
As shown in Figure 1, we can label each individual switch using the number 0 for off, and the number 1 for on. With this labeling, the setting for each switch corresponds to whether or not the finger is raised, and the result corresponds perfectly with our shorthand notation. All we need to do is number the switches from right to left, starting from zero (remember we normally count from zero in computing). Consider this configuration:
(1010)2
Our shorthand tells us that switch 0 (the rightmost one) is off, switch 1 is on, switch 2 is off, and switch 3 (the leftmost one) is on. The subscript is always one more than the number of fingers we have on one hand, and this number is more generally called the base. In this case, our base is 2, which means that we have a binary number represented by our shorthand. When we compute the value of this binary number in our normal base 10 system, we get its decimal equivalent. We perform the computation like this:
(1 * 23) + (0 * 22) + (1 * 21) + (0 * 20) =
(8)10 + (0)10 + (2)10 + (0)10 = (10)10
Note that the exponents correspond to the switch numbers, with switch 3 listed first, followed by 2, then 1, and finally 0. We raise the base to each exponent, then we multiply that result by the value of the corresponding switch to get the decimal value of each switch. Adding the individual decimal switch values together gives us the total value of the corresponding binary number.
General Formula for Base 10 Conversion
In general, any number expressed in a base other than 10 can be converted to base 10 using the following formula, extended with additional terms to the left as necessary:
(… stuv wxyz)B = … + (s * B7) + (t * B6) + (u * B5) + (v * B4) + (w * B3) + (x * B2) + (y * B1) + (z * B0) = (Value)10
In this formula, s, t, u, v, w, x, y, and z are individual digits in the original number, and B is the base of the original number. This formula will work for any arbitrary positive integer base.
While the algebra in the above formula might look intimidating, in practice, we only really use 4 bases in computing. These bases are 2 (binary), 8 (octal), 10 (decimal), and 16 (hexadecimal). As we’ve seen, binary is equivalent to counting with cheap robot hands, and hexadecimal corresponds to counting with our cool 15-fingered robot hands. Octal is the only base we haven’t seen yet, but these days, it is only really used for niche applications, such as Unix file permissions. Programming calculator applications are readily available for converting between these common bases.
All Your Base are Belong to Us
“All your base are belong to us” was an early Internet meme taken from poorly translated subtitles in the game Zero Wing.1
Table 3 summarizes the four most common number bases used in computing. While we can write number bases using our subscript notation, as mathematicians would do, computing literature often shortens things further by putting a prefix on any numbers that are not base 10. Thus, 0b0110 or just b0110 is equivalent to writing (0110)2. Similarly, writing #ffffff as a color in an HTML or CSS file is equivalent to (ffffff)16 (this form is not supported by HTML and CSS – you must use the prefix instead).
| Base | Name | Digits | Prefixes | Uses |
|---|---|---|---|---|
| 2 | Binary (Bin) |
0, 1 | 0b b |
Computer hardware internals |
| 8 | Octal (Oct) |
0, 1, 2, 3, 4, 5, 6, 7 | 0o o |
Unix file permissions |
| 10 | Decimal (Dec) |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | none d |
Ordinary numbers |
| 16 | Hexadecimal (Hex) |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F | 0x # |
HTML colors, binary shorthand |
Another use for hexadecimal is to explicitly refer to binary numbers without having to write them out the long way. For example, (1111 1111)16 can be more succinctly written as 0xff. Each f in the hexadecimal notation corresponds to a group of 1111 in the binary notation. Similarly, (1010 1010)2 can be more compactly written as 0xaa. Each group of 4 bits is independently converted to a single hexadecimal digit. This type of abbreviation using hexadecimal is common when performing low-level operations on hardware devices and in low-level application code.
The equivalencies of hexadecimal digits are sufficiently useful to warrant looking at them in detail. Table 4 shows these equivalencies.
| Hex Digit | Decimal | Binary | Octal |
|---|---|---|---|
| 0 | 0 | 0000 | 0 |
| 1 | 1 | 0001 | 1 |
| 2 | 2 | 0010 | 2 |
| 3 | 3 | 0011 | 3 |
| 4 | 4 | 0100 | 4 |
| 5 | 5 | 0101 | 5 |
| 6 | 6 | 0110 | 6 |
| 7 | 7 | 0111 | 7 |
| 8 | 8 | 1000 | 10 |
| 9 | 9 | 1001 | 11 |
| A | 10 | 1010 | 12 |
| B | 11 | 1011 | 13 |
| C | 12 | 1100 | 14 |
| D | 13 | 1101 | 15 |
| E | 14 | 1110 | 16 |
| F | 15 | 1111 | 17 |
To convert between hexadecimal and binary, work on single hexadecimal digits or binary groups of 4 digits. Thus, 0xffffff is equivalent to 0b1111 1111 1111 1111 1111 1111. Similarly, the binary 0b1010 0010 1011 0000 is equivalent to the hex 0xa2b0. For large numbers, hexadecimal is far more convenient than writing long binary sequences.
Notes and References
-
When Game Humor Attacks in Wired (2001). ↩
