
| Table of Contents
| Function Reference
| Function Finder
| R Project |
MULTIPLE REGRESSION
Preliminaries
Model Formulae
If you haven't yet read the tutorial on Model
Formulae, now would be a good time!
Statistical Modeling
There is not space in this tutorial, and probably not on this server, to
cover the complex issue of statistical modeling. For an excellent discussion, I
refer you to Chapter 9 of Crawley (2007).
Here I will restrict myself to a discussion of linear relationships. However,
transforming variables to make them linear (see
Simple Nonlinear Correlation and Regression) is straightforward, and a
model including interaction terms is as easily created as it is to change plus
signs to asterisks. (If you don't know what I'm talking about, read the Model Formulae tutorial.) R also includes a wealth of
tools for more complex modeling, among them...
- rlm( ) for robust fitting of linear models (MASS package)
- glm( ) for generalized linear models (stats package)
- gam( ) for generalized additive models (gam package)
- lme( ) and lmer( ) for linear mixed-effects models (nlme and lme4 packages)
- nls( ) and nlme( ) for nonlinear models (stats and nlme packages)
- and I'm sure there are others I'm leaving out
My familiarity with these functions is "less than thorough" (!), so I shall
refrain from mentioning them further.
Warning: An opinion follows! I am very much opposed to the current common
practice in the social sciences (and education) of "letting the software
decide" what statistical model is best. Statistical software is an assistant,
not a master. It should remain in the hands of the researcher or data analyst
which variables are retained in the model and which are excluded. Hopefully,
these decisions will be based on a thorough knowledge of the phenomenon being
modeled. Therefore, I will not discuss techniques such as stepwise regression
or hierarchical regression here. Stepwise regression is implemented in R (see
below for a VERY brief mention), and hierarchical regression (SPSS-like) can
easily enough be done, although it is not automated (that I am aware of). The
basic rule of statistical modeling should be: "all statistical models are wrong"
(George Box).
Letting the software have free reign to include and exclude model variables
in no way changes or improves upon that situation. It is not more "objective,"
and it does not result in better models, only less well understood ones.
Preliminary Examination of the Data
For this analysis, we will use a built-in data set called state.x77. It is
one of many helpful data sets R includes on the states of the U.S. However, it
is not a data frame, so after loading it, we will coerce it into being a data
frame.
> state.x77 # output not shown
> str(state.x77) # clearly not a data frame! (it's a matrix)
> st = as.data.frame(state.x77) # so we'll make it one
> str(st)
'data.frame': 50 obs. of 8 variables:
$ Population: num 3615 365 2212 2110 21198 ...
$ Income : num 3624 6315 4530 3378 5114 ...
$ Illiteracy: num 2.1 1.5 1.8 1.9 1.1 0.7 1.1 0.9 1.3 2 ...
$ Life Exp : num 69.0 69.3 70.5 70.7 71.7 ...
$ Murder : num 15.1 11.3 7.8 10.1 10.3 6.8 3.1 6.2 10.7 13.9 ...
$ HS Grad : num 41.3 66.7 58.1 39.9 62.6 63.9 56 54.6 52.6 40.6 ...
$ Frost : num 20 152 15 65 20 166 139 103 11 60 ...
$ Area : num 50708 566432 113417 51945 156361 ...
A couple things have to be fixed before this will be convenient to use, and
I also want to add a population density variable. Note that population density
is a linear function of Population and Area, so these three vectors will not be
linearly independent.
> colnames(st)[4] = "Life.Exp" # no spaces in variable names, please
> colnames(st)[6] = "HS.Grad" # ditto
> st$Density = st$Population * 1000 / st$Area # create a new column in st
If you are unclear on what these variables are, or want more information, see
the help page: ?state.x77.
A straightforward summary is always a good place to begin, because for one
thing it will find any variables that have missing values. Then, seeing as how
we are looking for interrelationships between these variables, we should look
at a correlation matrix, or perhaps a scatterplot matrix.
> summary(st)
Population Income Illiteracy Life.Exp Murder
Min. : 365 Min. :3098 Min. :0.500 Min. :67.96 Min. : 1.400
1st Qu.: 1080 1st Qu.:3993 1st Qu.:0.625 1st Qu.:70.12 1st Qu.: 4.350
Median : 2838 Median :4519 Median :0.950 Median :70.67 Median : 6.850
Mean : 4246 Mean :4436 Mean :1.170 Mean :70.88 Mean : 7.378
3rd Qu.: 4968 3rd Qu.:4814 3rd Qu.:1.575 3rd Qu.:71.89 3rd Qu.:10.675
Max. :21198 Max. :6315 Max. :2.800 Max. :73.60 Max. :15.100
HS.Grad Frost Area Density
Min. :37.80 Min. : 0.00 Min. : 1049 Min. : 0.6444
1st Qu.:48.05 1st Qu.: 66.25 1st Qu.: 36985 1st Qu.: 25.3352
Median :53.25 Median :114.50 Median : 54277 Median : 73.0154
Mean :53.11 Mean :104.46 Mean : 70736 Mean :149.2245
3rd Qu.:59.15 3rd Qu.:139.75 3rd Qu.: 81162 3rd Qu.:144.2828
Max. :67.30 Max. :188.00 Max. :566432 Max. :975.0033
>
> cor(st) # correlation matrix (not shown, yet)
> round(cor(st), 3) # rounding makes it easier to look at
Population Income Illiteracy Life.Exp Murder HS.Grad Frost Area Density
Population 1.000 0.208 0.108 -0.068 0.344 -0.098 -0.332 0.023 0.246
Income 0.208 1.000 -0.437 0.340 -0.230 0.620 0.226 0.363 0.330
Illiteracy 0.108 -0.437 1.000 -0.588 0.703 -0.657 -0.672 0.077 0.009
Life.Exp -0.068 0.340 -0.588 1.000 -0.781 0.582 0.262 -0.107 0.091
Murder 0.344 -0.230 0.703 -0.781 1.000 -0.488 -0.539 0.228 -0.185
HS.Grad -0.098 0.620 -0.657 0.582 -0.488 1.000 0.367 0.334 -0.088
Frost -0.332 0.226 -0.672 0.262 -0.539 0.367 1.000 0.059 0.002
Area 0.023 0.363 0.077 -0.107 0.228 0.334 0.059 1.000 -0.341
Density 0.246 0.330 0.009 0.091 -0.185 -0.088 0.002 -0.341 1.000
>
> pairs(st) # scatterplot matrix; plot(st) does the same thing
 That, gives us plenty to look at, doesn't it?
That, gives us plenty to look at, doesn't it?
I propose we cast "Life.Exp" into the role of our response variable and
attempt to model (predict) it from the other variables. Already we see some
interesting relationships. Life expectancy appears to be moderately to strongly
related to "Income" (positively), "Illiteracy" (negatively), "Murder"
(negatively), "HS.Grad" (positively), and "Frost" (no. of days per year with
frost, positively), and I call particular attention to this last relationship.
These are all bivariate relationships--i.e., they don't take into account any
of the remaining variables.
Here's another interesting relationship, which we would find statistically
significant. The correlation between average SAT scores by state and
average teacher pay by state is negative. That is to say, the states with higher
teacher pay have lower SAT scores. (How much political hay has been made of
that? These politicians either don't understand the nature of regression
relationships, or they are spinning the data to tell the story they want you
to hear!!) We would also find a very strong negative correlation between SAT
scores and percent of eligible students who take the test. I.e., the higher the
percentage of HS seniors who take the SAT, the lower the average score. Here is
the crucial point. Teacher pay is positively correlated with percent of students
who take the test. There is a potential confound here. In regression terms, we
would call percent of students who take the test a "lurking variable."
The advantage of looking at these variables in a multiple regression is we
are able to see the relationship between two variables with the others taken
out. To say this another way, the regression analysis "holds the potential
lurking variables constant" while it is figuring out the relationship between
the variables of interest. When SAT scores, teacher pay, and percent taking the
test are all entered into the regression relationship, the confound between
pay and percent is controlled, and the relationship between teacher pay and SAT
scores is shown to be significantly positive. (Note: If you get the Faraway
data sets when we do the ANCOVA tutorial, you will
have a data set, sat.txt, that will allow you to examine this. It's an
interesting problem and a recommended exercise.)
The point of this long discussion is this. Life expectancy does have a
bivariate relationship with a lot of the other variables, but many of those
variables are also related to each other. Multiple regression allows us to tease
all of this apart and see in a "purer" (but not pure) form what the relationship
really is between, say, life expectancy and average number of days with frost. I
suggest you watch this relationship as we proceed through the analysis.
We should also examine the variables for outliers and distribution before
proceeding, but for the sake of brevity, we'll skip it. But a quick way to do
it all at once would be:
> par(mfrow=c(3,3))
> for(i in 1:9) qqnorm(st[,i], main=colnames(st)[i])
The Maximal or Full Model (Sans Interactions)
We begin by throwing all the predictors into a linear additive model.
> options(show.signif.stars=F) # I don't like significance stars!
> names(st) # for handy reference
[1] "Population" "Income" "Illiteracy" "Life.Exp" "Murder"
[6] "HS.Grad" "Frost" "Area" "Density"
> ### model1 = lm(Life.Exp ~ Population + Income + Illiteracy + Murder +
+ ### HS.Grad + Frost + Area + Density, data=st)
> ### This is what we're going to accomplish, but more economically, by
> ### simply placing a dot after the tilde, which means "everything else."
> model1 = lm(Life.Exp ~ ., data=st)
> summary(model1)
Call:
lm(formula = Life.Exp ~ ., data = st)
Residuals:
Min 1Q Median 3Q Max
-1.47514 -0.45887 -0.06352 0.59362 1.21823
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.995e+01 1.843e+00 37.956 < 2e-16
Population 6.480e-05 3.001e-05 2.159 0.0367
Income 2.701e-04 3.087e-04 0.875 0.3867
Illiteracy 3.029e-01 4.024e-01 0.753 0.4559
Murder -3.286e-01 4.941e-02 -6.652 5.12e-08
HS.Grad 4.291e-02 2.332e-02 1.840 0.0730
Frost -4.580e-03 3.189e-03 -1.436 0.1585
Area -1.558e-06 1.914e-06 -0.814 0.4205
Density -1.105e-03 7.312e-04 -1.511 0.1385
Residual standard error: 0.7337 on 41 degrees of freedom
Multiple R-squared: 0.7501, Adjusted R-squared: 0.7013
F-statistic: 15.38 on 8 and 41 DF, p-value: 3.787e-10
It appears higher populations are related to increased life expectancy and
higher murder rates are strongly related to decreased life expectancy. High
school graduation rate is marginal. Other
than that, we're not seeing much. Another kind of summary of the model can be
obtained like this.
> summary.aov(model1)
Df Sum Sq Mean Sq F value Pr(>F)
Population 1 0.4089 0.4089 0.7597 0.388493
Income 1 11.5946 11.5946 21.5413 3.528e-05
Illiteracy 1 19.4207 19.4207 36.0811 4.232e-07
Murder 1 27.4288 27.4288 50.9591 1.051e-08
HS.Grad 1 4.0989 4.0989 7.6152 0.008612
Frost 1 2.0488 2.0488 3.8063 0.057916
Area 1 0.0011 0.0011 0.0020 0.964381
Density 1 1.2288 1.2288 2.2830 0.138472
Residuals 41 22.0683 0.5383
These are sequential tests on the terms, as if they were entered one at a
time in a hierarchical fashion, beginning with Population by itself, then
Income added to Population, then Illiteracy added to Population and Income,
etc. Notice that the test on Density yields the same p-value, because in the
sequential tests it is entered last, after everything else, just as it is (and
all the other terms are) in the regression analysis. Make what you will of
these tests. I'm not saying they aren't useful or interesting, but I won't be
referring to them again.
A note on interactions. What about the possibility that there might
be important interactions between some of these terms? It's a legitimate
question, and I'll address it in a little bit, but including interactions in
a regression model raises some special issues. In this case particularly, it
would probably be a bad idea to test too many because of the linear dependence
among some of our variables. Even without that problem though, testing
interactions usually involves centering the variables, AND just imagine how
many of them there would be! Plus, interpreting higher order interactions can
be difficult, to say the least. I think we need to simplify our model a bit
before we start fooling with interactions. I will mention them again below.
Now we need to start winnowing down our model to a minimal adequate one. The
least significant of the slopes in the above summary table (two tables ago--NOT
the sequential ANOVA table) was that for
"Illiteracy", so some would say that term must go first. I beg to differ. Rather
than letting a bunch of (I assume) insentient electrons make this decision for
me, I'm going to take matters into my own (hopefully) capable hands and let the
sodium and potassium ions in my brain make the decision. I should decide, not
the machine. The machine is my assistant, not my boss!
I like the "Illiteracy" term, and I can see how it might well be related to
life expectancy. I cannot see how "Area" of the state in which a person lives
could be related, except in that it might be confounded with something else.
"Area" has almost as high a p-value as "Illiteracy", so that is the first term
I am going to toss from my model.
The Minimal Adequate Model
We want to reduce our model to a point where all the remaining predictors
are significant, and we want to do this by throwing out one predictor at a time.
"Area" will go first. To do this, we could just recast the model without the
"Area" variable, but R supplies a handier way.
> model2 = update(model1, .~. -Area)
> summary(model2)
Call:
lm(formula = Life.Exp ~ Population + Income + Illiteracy + Murder +
HS.Grad + Frost + Density, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.5025 -0.4047 -0.0608 0.5868 1.4386
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.094e+01 1.378e+00 51.488 < 2e-16
Population 6.249e-05 2.976e-05 2.100 0.0418
Income 1.485e-04 2.690e-04 0.552 0.5840
Illiteracy 1.452e-01 3.512e-01 0.413 0.6814
Murder -3.319e-01 4.904e-02 -6.768 3.12e-08
HS.Grad 3.746e-02 2.225e-02 1.684 0.0996
Frost -5.533e-03 2.955e-03 -1.873 0.0681
Density -7.995e-04 6.251e-04 -1.279 0.2079
Residual standard error: 0.7307 on 42 degrees of freedom
Multiple R-squared: 0.746, Adjusted R-squared: 0.7037
F-statistic: 17.63 on 7 and 42 DF, p-value: 1.173e-10
The syntax of update() is cryptic, so here's what
it means. Inside the
new formula, a dot means "same." So read the above update command as follows:
"Update model1 using the same response variables and the same predictor
variables, except remove (minus) "Area". Notice that removing "Area" has cost
us very little in terms of R-squared, and the adjusted R-squared actually went
up, due to there being fewer predictors. The two models can be compared as
follows.
> anova(model2, model1) # enter the name of the reduced model first
Analysis of Variance Table
Model 1: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Density
Model 2: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Area + Density
Res.Df RSS Df Sum of Sq F Pr(>F)
1 42 22.425
2 41 22.068 1 0.35639 0.6621 0.4205
As you can see, removing "Area" had no significant effect on the model
(p = .4205). Compare the p-value to that for "Area" in the first
summary table above.
What goes next, "Income" or "Illiteracy"? I can see how either one of these
could be related to life expectancy. In fact, the only one of these variables
I'm a little leary of at this point is "Frost". But I'm also intrigued by it,
and it is close to being significant. So, my assistant is telling me to toss
out "Illiteracy", and reluctantly I agree.
> model3 = update(model2, .~. -Illiteracy)
> summary(model3)
Call:
lm(formula = Life.Exp ~ Population + Income + Murder + HS.Grad +
Frost + Density, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.49555 -0.41246 -0.05336 0.58399 1.50535
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.131e+01 1.042e+00 68.420 < 2e-16
Population 5.811e-05 2.753e-05 2.110 0.0407
Income 1.324e-04 2.636e-04 0.502 0.6181
Murder -3.208e-01 4.054e-02 -7.912 6.32e-10
HS.Grad 3.499e-02 2.122e-02 1.649 0.1065
Frost -6.191e-03 2.465e-03 -2.512 0.0158
Density -7.324e-04 5.978e-04 -1.225 0.2272
Residual standard error: 0.7236 on 43 degrees of freedom
Multiple R-squared: 0.745, Adjusted R-squared: 0.7094
F-statistic: 20.94 on 6 and 43 DF, p-value: 2.632e-11
Things are starting to change a bit. R-squared went down again, as it will
always do when a predictor is removed, but once more, adjusted R-squared
increased. "Frost" is also now a significant predictor of life expectancy, and
unlike in the bivariate relationship we saw originally, the relationship is now
negative.
Looks like "Income" should go next, but gosh darn it, how can income not be
related to life expectancy? Well, you have to be careful how you say that. The
model is NOT telling us that income is unrelated to life expectancy! It's telling
us that, within the parameters of this model, "Income" is now the worst
predictor. A look back at the correlation matrix shows that "Income" is strongly
correlated with "HS.Grad". Maybe "HS.Grad" is stealing some its thunder. On the
other hand, income is important because it can buy you things, like a house in a
neighborhood with good schools and low murder rate, and in the "burbs" (lower
population density). Sorry "Income" but I gotta give you the ax. (NOTE: The
important thing is, I thought about it and came to this conclusion rationally. I
didn't blindly let the numbers tell me what to do--entirely.)
> model4 = update(model3, .~. -Income)
> summary(model4)
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost +
Density, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.56877 -0.40951 -0.04554 0.57362 1.54752
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.142e+01 1.011e+00 70.665 < 2e-16
Population 6.083e-05 2.676e-05 2.273 0.02796
Murder -3.160e-01 3.910e-02 -8.083 3.07e-10
HS.Grad 4.233e-02 1.525e-02 2.776 0.00805
Frost -5.999e-03 2.414e-03 -2.485 0.01682
Density -5.864e-04 5.178e-04 -1.132 0.26360
Residual standard error: 0.7174 on 44 degrees of freedom
Multiple R-squared: 0.7435, Adjusted R-squared: 0.7144
F-statistic: 25.51 on 5 and 44 DF, p-value: 5.524e-12
R-squared went down hardly at all. Adjusted R-squared went up. "Income" will
not be missed FROM THIS MODEL. Now all the predictors are significant except
"Density", and while my heart says stay, I have to admit that looking at the
correlation matrix tells me "Density" isn't really strongly related to
anything.
> model5 = update(model4, .~. -Density)
> summary(model5)
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost,
data = st)
Residuals:
Min 1Q Median 3Q Max
-1.47095 -0.53464 -0.03701 0.57621 1.50683
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.103e+01 9.529e-01 74.542 < 2e-16
Population 5.014e-05 2.512e-05 1.996 0.05201
Murder -3.001e-01 3.661e-02 -8.199 1.77e-10
HS.Grad 4.658e-02 1.483e-02 3.142 0.00297
Frost -5.943e-03 2.421e-03 -2.455 0.01802
Residual standard error: 0.7197 on 45 degrees of freedom
Multiple R-squared: 0.736, Adjusted R-squared: 0.7126
F-statistic: 31.37 on 4 and 45 DF, p-value: 1.696e-12
Adjusted R-squared slipped a bit that time, but not significantly as we could
confirm by...
> anova(model5, model4) # output not shown
What I really want to do here is compare this model to the original full
model.
> anova(model5, model1)
Analysis of Variance Table
Model 1: Life.Exp ~ Population + Murder + HS.Grad + Frost
Model 2: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Area + Density
Res.Df RSS Df Sum of Sq F Pr(>F)
1 45 23.308
2 41 22.068 4 1.2397 0.5758 0.6818
It looks like we have lost nothing of significance, so to speak. I.e., the two
models are not significantly different.
We have (implicitly by not saying otherwise) set our alpha level at .05, so
now "Population" must go. So say the bean counters. This could have a substantial
effect on the model, as the slope for "Population" is very nearly significant.
We already know that creating a model without it and comparing it to the current
model (model5) would result in a p-value of 0.052. Gosh, it's so close! But as
my old stat professor (Tom Wickens) would say, close only counts in horseshoes
and handgrenades. I have to disagree. I am not one of those who worships the
magic number point-oh-five. I don't see much difference between 0.052 and 0.048.
Before we make this decision, let's look at something else first.
I raised the issue of interactions above. Is it possible that there are some
interactions among these variables that might be important? Granted, we've
already tossed out quite a few of the variables, so maybe it's a little late to
be asking, but better late than never. (You can quote me!) Now that we have few
enough terms where interactions might start to make sense, let's test them all
at once. I will test everything up to the three-way interactions. I'm not
leaving out the four-way interaction for any good reason other than to
demonstrate that I can. Include it if you want.
> model.int = update(model5, .~.^3)
> anova(model5, model.int)
Analysis of Variance Table
Model 1: Life.Exp ~ Population + Murder + HS.Grad + Frost
Model 2: Life.Exp ~ Population + Murder + HS.Grad + Frost + Population:Murder +
Population:HS.Grad + Population:Frost + Murder:HS.Grad +
Murder:Frost + HS.Grad:Frost + Population:Murder:HS.Grad +
Population:Murder:Frost + Population:HS.Grad:Frost + Murder:HS.Grad:Frost
Res.Df RSS Df Sum of Sq F Pr(>F)
1 45 23.308
2 35 15.869 10 7.4395 1.6409 0.1356
In a model formula, ^ is a way to specify interactions, so .^3 means include
all the terms in the current model (the dot) and all interactions up to
three-way. If you want to limit it to two-way, then use .^2. If you want the
four-way, then it's .^4. It appears from our resultant comparison of the models
with and without the interactions, that the interactions do not make a
significant contribution to the model. So I'm not going to worry about them
further.
Now we have to make a decision about "Population". My gut says it should
stay, and it's a pretty substantial gut! But to keep the point-oh-fivers
happy, let's get rid of it.
> model6 = update(model5, .~. -Population)
> summary(model6)
Call:
lm(formula = Life.Exp ~ Murder + HS.Grad + Frost, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.5015 -0.5391 0.1014 0.5921 1.2268
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 71.036379 0.983262 72.246 < 2e-16
Murder -0.283065 0.036731 -7.706 8.04e-10
HS.Grad 0.049949 0.015201 3.286 0.00195
Frost -0.006912 0.002447 -2.824 0.00699
Residual standard error: 0.7427 on 46 degrees of freedom
Multiple R-squared: 0.7127, Adjusted R-squared: 0.6939
F-statistic: 38.03 on 3 and 46 DF, p-value: 1.634e-12
We have reached the minimal adequate model in which all the slopes are
statistically significant.
Stepwise Regression
What we did in the previous section can be automated using the
step() function.
> step(model1, direction="backward")
Start: AIC=-22.89
Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Area + Density
Df Sum of Sq RSS AIC
- Illiteracy 1 0.305 22.373 -24.208
- Area 1 0.356 22.425 -24.093
- Income 1 0.412 22.480 -23.969
<none> 22.068 -22.894
- Frost 1 1.110 23.178 -22.440
- Density 1 1.229 23.297 -22.185
- HS.Grad 1 1.823 23.891 -20.926
- Population 1 2.510 24.578 -19.509
- Murder 1 23.817 45.886 11.706
Step: AIC=-24.21
Life.Exp ~ Population + Income + Murder + HS.Grad + Frost + Area +
Density
Df Sum of Sq RSS AIC
- Area 1 0.143 22.516 -25.890
- Income 1 0.232 22.605 -25.693
<none> 22.373 -24.208
- Density 1 0.929 23.302 -24.174
- HS.Grad 1 1.522 23.895 -22.917
- Population 1 2.205 24.578 -21.508
- Frost 1 3.132 25.506 -19.656
- Murder 1 26.707 49.080 13.072
Step: AIC=-25.89
Life.Exp ~ Population + Income + Murder + HS.Grad + Frost + Density
Df Sum of Sq RSS AIC
- Income 1 0.132 22.648 -27.598
- Density 1 0.786 23.302 -26.174
<none> 22.516 -25.890
- HS.Grad 1 1.424 23.940 -24.824
- Population 1 2.332 24.848 -22.962
- Frost 1 3.304 25.820 -21.043
- Murder 1 32.779 55.295 17.033
Step: AIC=-27.6
Life.Exp ~ Population + Murder + HS.Grad + Frost + Density
Df Sum of Sq RSS AIC
- Density 1 0.660 23.308 -28.161
<none> 22.648 -27.598
- Population 1 2.659 25.307 -24.046
- Frost 1 3.179 25.827 -23.030
- HS.Grad 1 3.966 26.614 -21.529
- Murder 1 33.626 56.274 15.910
Step: AIC=-28.16
Life.Exp ~ Population + Murder + HS.Grad + Frost
Df Sum of Sq RSS AIC
<none> 23.308 -28.161
- Population 1 2.064 25.372 -25.920
- Frost 1 3.122 26.430 -23.876
- HS.Grad 1 5.112 28.420 -20.246
- Murder 1 34.816 58.124 15.528
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost, data = st)
Coefficients:
(Intercept) Population Murder HS.Grad Frost
7.103e+01 5.014e-05 -3.001e-01 4.658e-02 -5.943e-03
I'm against it! Having said that, I have to point out that the stepwise
regression reached the same model we did, through almost the same sequence of
steps, EXCEPT it kept the population term. This procedure does not make decisions
based on p-values but on a statistic called AIC (Akaike's Information Criterion,
which is like a golf score in that lower values are better). Notice in the last
step, the model throwing out nothing had an AIC of -28.161. If "Population"
is thrown out, that rises (bad!) to -25.920. So "Population" was retained. I
hate to say I told you so, especially based on a method I don't believe in,
but there you go. In the stepwise() function,
the "direction=" option can be set to "forward", "backward", or "both".
Confidence Limits on the Estimated Coefficients
I'm going to work with model5.
> confint(model5)
2.5 % 97.5 %
(Intercept) 6.910798e+01 72.9462729104
Population -4.543308e-07 0.0001007343
Murder -3.738840e-01 -0.2264135705
HS.Grad 1.671901e-02 0.0764454870
Frost -1.081918e-02 -0.0010673977
Set the desired confidence level with the "level=" option (not conf.level as in
many other R functions).
Predictions
Predictions can be made from a model equation using the
predict() function.
> predict(model5, list(Population=2000, Murder=10.5, HS.Grad=48, Frost=100))
1
69.61746
Feed it the model name and a list of labeled values for the predictors.
The values to be predicted from can be vectors.
Regression Diagnostics
The usual diagnostic plots are available.
> par(mfrow=c(2,2)) # visualize four graphs at once
> plot(model5)
> par(mfrow=c(1,1)) # reset the graphics defaults
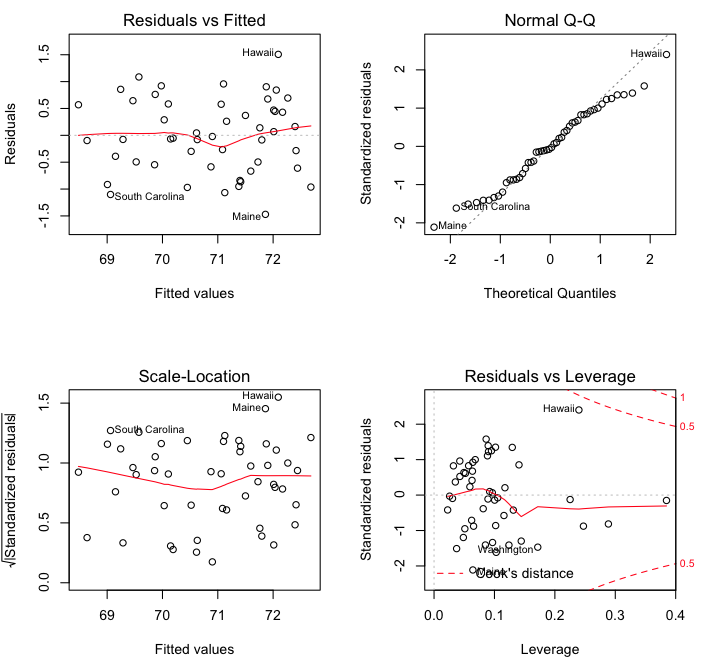 The first of these plots (upper left) is a standard residuals plot with which
we can evaluate linearity (looks good) and homoscedasticity (also good). The
second plot (upper right) is a normal quantile plot of the residuals, which
should be normally distributed. We have a little deviation from normality
in the tails,
but it's not too bad. The scale-location plot is supposedly a more sensitive
way to look for heteroscedasticity, but I've never found it very useful, to
be honest. The last plot shows possible high leverage and influential cases.
These graphs could also be obtained with the following commands.
The first of these plots (upper left) is a standard residuals plot with which
we can evaluate linearity (looks good) and homoscedasticity (also good). The
second plot (upper right) is a normal quantile plot of the residuals, which
should be normally distributed. We have a little deviation from normality
in the tails,
but it's not too bad. The scale-location plot is supposedly a more sensitive
way to look for heteroscedasticity, but I've never found it very useful, to
be honest. The last plot shows possible high leverage and influential cases.
These graphs could also be obtained with the following commands.
> plot(model5, 1) # syntax: plot(model.object.name, 1)
> plot(model5, 2)
> plot(model5, 3)
> plot(model5, 5)
There is also plot(model5, 4), which gives a
Cook's Distance plot.
Extracting Elements of the Model Object
The model object is a list containing quite a lot of information.
> names(model5)
[1] "coefficients" "residuals" "effects" "rank" "fitted.values"
[6] "assign" "qr" "df.residual" "xlevels" "call"
[11] "terms" "model"
There are three ways to get at this information that I'm aware of.
> coef(model5) # an extractor function
(Intercept) Population Murder HS.Grad Frost
7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03
> model5$coefficients # list indexing
(Intercept) Population Murder HS.Grad Frost
7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03
> model5[[1]] # recall by position in the list (double brackets for lists)
(Intercept) Population Murder HS.Grad Frost
7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03
Aside from the coefficients, the residuals are the most interesting (to me).
Just enough of the list item name has to be given so that R can recognize what
it is you're asking for.
> model5$resid
Alabama Alaska Arizona Arkansas California
0.56888134 -0.54740399 -0.86415671 1.08626119 -0.08564599
Colorado Connecticut Delaware Florida Georgia
0.95645816 0.44541028 -1.06646884 0.04460505 -0.09694227
Hawaii Idaho Illinois Indiana Iowa
1.50683146 0.37010714 -0.05244160 -0.02158526 0.16347124
Kansas Kentucky Louisiana Maine Maryland
0.67648037 0.85582067 -0.39044846 -1.47095411 -0.29851996
Massachusetts Michigan Minnesota Mississippi Missouri
-0.61105391 0.76106640 0.69440380 -0.91535384 0.58389969
Montana Nebraska Nevada New Hampshire New Jersey
-0.84024805 0.42967691 -0.49482393 -0.49635615 -0.66612086
New Mexico New York North Carolina North Dakota Ohio
0.28880945 -0.07937149 -0.07624179 0.90350550 -0.26548767
Oklahoma Oregon Pennsylvania Rhode Island South Carolina
0.26139958 -0.28445333 -0.95045527 0.13992982 -1.10109172
South Dakota Tennessee Texas Utah Vermont
0.06839119 0.64416651 0.92114057 0.84246817 0.57865019
Virginia Washington West Virginia Wisconsin Wyoming
-0.06691392 -0.96272426 -0.96982588 0.47004324 -0.58678863
Here is a particularly interesting way to look at the residuals.
> sort(model5$resid) # extract residuals and sort them
Maine South Carolina Delaware West Virginia Washington
-1.47095411 -1.10109172 -1.06646884 -0.96982588 -0.96272426
Pennsylvania Mississippi Arizona Montana New Jersey
-0.95045527 -0.91535384 -0.86415671 -0.84024805 -0.66612086
Massachusetts Wyoming Alaska New Hampshire Nevada
-0.61105391 -0.58678863 -0.54740399 -0.49635615 -0.49482393
Louisiana Maryland Oregon Ohio Georgia
-0.39044846 -0.29851996 -0.28445333 -0.26548767 -0.09694227
California New York North Carolina Virginia Illinois
-0.08564599 -0.07937149 -0.07624179 -0.06691392 -0.05244160
Indiana Florida South Dakota Rhode Island Iowa
-0.02158526 0.04460505 0.06839119 0.13992982 0.16347124
Oklahoma New Mexico Idaho Nebraska Connecticut
0.26139958 0.28880945 0.37010714 0.42967691 0.44541028
Wisconsin Alabama Vermont Missouri Tennessee
0.47004324 0.56888134 0.57865019 0.58389969 0.64416651
Kansas Minnesota Michigan Utah Kentucky
0.67648037 0.69440380 0.76106640 0.84246817 0.85582067
North Dakota Texas Colorado Arkansas Hawaii
0.90350550 0.92114057 0.95645816 1.08626119 1.50683146
That settles it! I'm moving to Hawaii. This could all just be random error, of
course, but more technically, it is unexplained variation. It could mean that
Maine is performing the worst against our model, and Hawaii the best, due to
factors we have not included in the model.
Beta Coefficients
Beta or standardized coefficients are the slopes we would get if all the
variables were on the same scale, which is done by converting them to z-scores
before doing the regression. Betas allow a comparison of the approximate
relative importance of the predictors, which neither the unstandardized
coefficients nor the p-values do. Scaling, or standardizing, the data vectors
can be done using the scale() function. Once the
scaled variables are created, the regression is redone using them. The
resulting coefficients are the beta coefficients.
That sounds like a lot of fuss and bother, so here is the way I do it. It's
based on the fact that a coefficient times the standard deviation of that
variable divided by the standard deviation of the response variable gives the
beta coefficient for the variable.
> coef(model5)
(Intercept) Population Murder HS.Grad Frost
7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03
> sdexpl = c(sd(st$Population), sd(st$Murder), sd(st$HS.Grad), sd(st$Frost))
> sdresp = sd(st$Life.Exp)
> coef(model5)[2:5] * sdexpl / sdresp
Population Murder HS.Grad Frost
0.1667540 -0.8253997 0.2802790 -0.2301391
So an increase of one standard deviation in the murder rate is associated with a
drop of 0.825 standard deviations in life expectancy, if all the other variables
are held constant. VERY roughly and approximately, these values can be
interpreted as
correlations with the other predictors controlled. We can see that HS.Grad and
Frost are of roughly the same importance in predicting Life.Exp. Population is
about right in there with them, or maybe a little less. Clearly, in our model,
Murder is the most important predictor of Life.Exp.
Partial Correlations
Another way to remove the effect of a possible lurking variable from the
correlation of two other variables is to calculate a partial correlation. There
is no partial correlation function in R base packages. There are optional
packages that have such functions, including the package "ggm", in which
the function is pcor().
Making Predictions From a Model
To illustrate how predictions are made from a model, I will fit a new model to
another data set.
> rm(list=ls()) # clean up (WARNING! this will wipe your workspace!)
> data(airquality) # see ?airquality for details on these data
> na.omit(airquality) -> airquality # toss cases with missing values
> lm.out = lm(Ozone ~ Solar.R + Wind + Temp + Month, data=airquality)
> coef(lm.out)
(Intercept) Solar.R Wind Temp Month
-58.05383883 0.04959683 -3.31650940 1.87087379 -2.99162786
> confint(lm.out)
2.5 % 97.5 %
(Intercept) -1.035964e+02 -12.51131722
Solar.R 3.088529e-03 0.09610512
Wind -4.596849e+00 -2.03616955
Temp 1.328372e+00 2.41337586
Month -5.997092e+00 0.01383629
The model has been fitted and the regression coefficients displayed. Suppose
now we wish to predict for new values: Solar.R=200, Wind=11, Temp=80, Month=6.
One way to do this is as follows.
> (prediction = c(1, 200, 11, 80, 6) * coef(lm.out))
(Intercept) Solar.R Wind Temp Month
-58.053839 9.919365 -36.481603 149.669903 -17.949767
> ### Note: putting the whole statement in parentheses not only stores the values
> ### but also prints them to the Console.
> ### Now we have the contribution of each variable to the prediction. It remains
> ### but to sum them.
> sum(prediction)
[1] 47.10406
Our predicted value is 47.1. How accurate is it?
We can get a confidence interval for the predicted value, but first we have to
ask an important question. Is the prediction being made for the mean response for
cases like this? Or is it being made for a new single case? The difference this
makes to the CI is shown below.
> ### Prediction of mean response for cases like this...
> predict(lm.out, list(Solar.R=200, Wind=11, Temp=80, Month=6), interval="conf")
fit lwr upr
1 47.10406 41.10419 53.10393
> ### Prediction for a single new case...
> predict(lm.out, list(Solar.R=200, Wind=11, Temp=80, Month=6), interval="pred")
fit lwr upr
1 47.10406 5.235759 88.97236
As you can see, the CI is much wider in the second case. These are 95% CIs. You
can set a different confidence level using the "level=" option. The function
predict() has a somewhat tricky syntax,
so here's how it works. The first
argument should be the name of the model object. The second argument should be
a list of new data values labeled with the variable names. That's all
that's really required. The "interval=" option can take values of "none" (the
default), "confidence", or "prediction". You need only type enough of it so R
knows which one you want. The confidence level is changed with the "level="
option, and not with "conf.level=" as in other R functions.
Sooooo, when we did confint(lm.out) above,
what are those confidence limits? Are they for predicting the mean response
for cases like this? Or for predicting for a single new case? Let's find out!
> intervals = confint(lm.out)
> t(intervals)
(Intercept) Solar.R Wind Temp Month
2.5 % -103.59636 0.003088529 -4.596849 1.328372 -5.99709200
97.5 % -12.51132 0.096105125 -2.036170 2.413376 0.01383629
> values = c(1,200,11,80,6)
> sum(colMeans(t(intervals)) * values)
[1] 47.10406
> t(intervals) %*% matrix(values)
[,1]
2.5 % -83.25681
97.5 % 177.46493
Neither!
revised 2016 February 17
| Table of Contents
| Function Reference
| Function Finder
| R Project |
|


