The problem with comparing scores on a history exam to scores on a math exam is that often the scales on which the exams were scored will be different. Even if both tests were 100-point exams, the comparison may be faulty because the means and standard deviations will be different. Standard scores are a way of taking scores from different scales and putting them on the same scale. The most common standard score is the z-score, which technically is calculated as follows:

However, in practice we rarely ever have these population parameters (mu and sigma, the population mean and population standard deviation), so the sample statistics are substituted for them.

It's important to remember that turning raw scores into standard scores does not normalize the distribution of the scores (does not change a skewed distribution to a normal distribution, for example), a common misconception of beginning students, as they most often learn about standard scores in conjunction with the standard normal distribution. Since the z-score formula represents a linear transformation of raw scores, the shape of the raw score distribution will not change.

Other common standard scores are shown in the following illustration. They are shown in conjunction with how they divide up a normal distribution, but it is not necessary to have a normal distribution to calculate any of them.

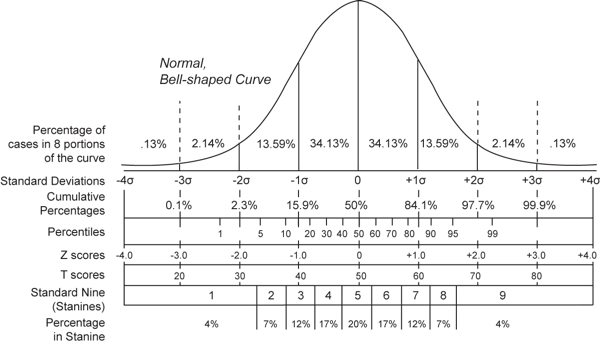
source: http://en.wikipedia.org/wiki/Standard_score

Z-scores are "pure numbers" (have no units of measurement attached to them). When scores are expressed as z-scores, we are essentially measuring how many standard deviations away from the mean a certain raw score falls. Thus, z=1.28 indicates a raw score that is 1.28 standard deviations above the mean, while z=-2.07 indicates a raw score that is 2.07 standard deviations below the mean.