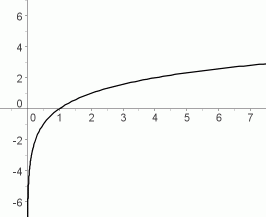
Logarithmic functions have the general form y = a + b log(x). (From here on we will always assume natural logs, or base e logs, unless explicitly stated otherwise.) Such functions have two important characteristics.

1) They are monotonic, which is to say, the graph is always increasing or always decreasing. It never changes directions as it can for a polynomial function.
2) The rate of change decreases as x becomes larger. I.e, as x gets bigger, the brakes are put on y. (Not a bad metaphor because such graphs are called decelerating.) This causes the graph to appear to approach a horizonal asymptote as x gets larger. (It doesn't really.)

Graph of a Logarithmic Function

Exponential function means the variable x is an exponent of some base. It is always possible, and often practical, to change this base to e, and we will always do so (or assume the base is e). Thus, the general form of an exponential function is:

y = ae^bx

Statistically, this function is more useful if we take the log of both sides...

log(y) = log(ae^bx)
log(y) = log(a) + log(e^bx)
log(y) = a₀ + bx (where log(a) = a₀)

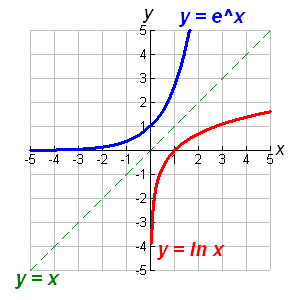
The following graph shows the relationship between log functions and exponential functions. (Note: log to the base e is sometimes denoted as ln.)

Power functions also involve logs, in this case of both x and y. For our purposes, the general form of a power function is:

log(y) = a + b log(x)

Other nonlinear functions include y = f(1/x) and y = f(sqrt(x)).