Vectors in the Plane
1. Let \({\bf a}\) be a standard position
vector with terminal point (-2,-4). Let \({\bf b}\) be a vector with
initial point (1,2) and terminal point (-1,4) . Find the magnitude
of the vector \({\bf a} - 3{\bf b} -4{\bf i}+ {\bf j}\).
SOLUTION
2. Find a unit vector in the same direction as \(\overrightarrow{v} =
4 \overrightarrow{i}- 3 \overrightarrow{j} \).
SOLUTION
3. A vector \(\overrightarrow{v}\) has initial
point \((-1, 3)\) and terminal point \((4, -9)\). Find the unit vector
in the direction of \(\overrightarrow{v}\). Express your answer in
component form.
SOLUTION
4. Consider points \( P(-1, 2) \), \(Q(3, 5),\)
and \( R(4, 14)\). Determine the following vectors in the
component form.
SOLUTION
(a) \(\overrightarrow{PQ} + \overrightarrow{PR}
\). (b) The unit vector in the direction of
\(\overrightarrow{PQ}\). (c) The unit vector in the direction of
\(\overrightarrow{PR}\).
5. Find the component form of the vector \( \bf
v \) with the given magnitude and in the same direction as vector
\( \bf u\). \( |{\bf v}| = 8, \: {\bf u} =
\langle -3, 4 \rangle \)
SOLUTION
6. Find the component form of the vector
\( \overrightarrow{u}\), given its magnitude and the angle, \(\theta\),
that it forms with the positive x-axis. \(
|\overrightarrow{u}| = 8, \quad \theta =\frac{3\pi}{4}\)
SOLUTION
7.
Find the angle \(\theta \in [0, 2\pi] \) that the vector \(
{\bf u}\) makes with the positive direction of the x-axis, in a
counter-clockwise direction. \( {\bf u} = 2{\bf
i}-2\sqrt 3{\bf j} \)
SOLUTION
A plane has a heading \(35^0\) south of east at 500 mph. The wind speed is 25 mph wtih direction \(40^0\) south of west. Find the ground speed, direction and drift angle.
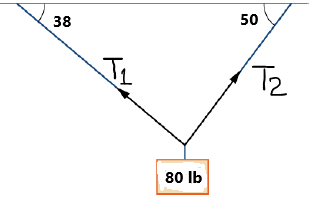
9. A 80-lb weight is hung by a cable so
that the two portions of the cable make angles of \(38^\circ\) and
\(50^\circ\), respectively, with the horizontal. Find the magnitudes of
the forces of tension \(T_1\) and \(T_2\) in the cables if the resultant
force acting on the object is zero.
SOLUTION