Area of regions between curves

  1. Find the area between the curves \( f(x)=x \) and \( g(x)=x^2\).  solution

  2. Find the area between the curves \( y=2x-1 \) and \( y=x^2-1\).  solution

  3. Find the area between the curves as shown.  solution

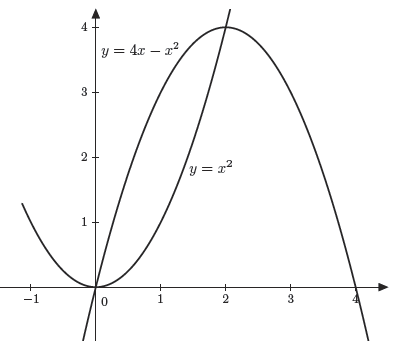
    4. graph3

  4. Find the area under the curve \( y=x\) on the interval \( [0,4]\).   solution

  5. Find the area of the region enclosed by the curves \(y=\sqrt{x}, \; y=0\) and \(x=9\) by setting up a definite integral (a) in terms of \(x\) alone, (b) in terms of \( y\) alone.

  6. Find the area of the region bounded by the curve \(f(x)=3x-x^2, \) and the \(x\)-axis.   solution

  7. Find the area of the region bounded by the curves \(y=\sqrt{x},   x=5\) and the \(x\)-axis.   solution

  8. Find the area of the region bounded by the curves: \( y=x^3 \) and \( y= x \).  solution

  9. Find the area of the region bounded by the curves: \( y=x^2 \) and \( y=4x-x^2\).  solution

  10. Find the area of the region bounded by the curves: \( y=\sqrt{x}\) and  \( y=x^2\).  solution

  11. Find the area of the region bounded by the curves: \( y=\sqrt{x},  y=x^2\) and \(x=2\).   solution

  12. Compute the area of the region bounded by the curves \( y^2=x \) and \( y=2-x\).  solution

  13. Find the area of the region bounded by the curves: \( x=y^2 \) and \( x=8-y^2\).  solution

  14. Find the area of the region bounded by the curves \(y=\sec ^{2} x, \: y=6 \cos x, \, \, -\pi / 4 \leq x \leq \pi / 4 \).  solution

  15. Find the area bounded by the curves \(y=e^x\) and \(y=x e^{x^2}\) between \(x=0\) and \(x=1\).  solution

  16. Draw the region bounded by the curves, and find its area. \( y = 3/x, \, y=12x, \, y=x/3, \, x \ge 0.\)  solution