Fundamental Theorem of Calculus

  1. Find the derivative, \(g'(x) \), of each of the following functions. solution

    2. (a) \( \displaystyle g(x) =\int_2^x (5t-\ln t + 7) \,  dt \)     (b) \( \displaystyle  g(x) =\int_x^4 \frac{\tan t}{1+t^2} \,  dt \)     (c) \( \displaystyle  g(x) =\int_5^x \sqrt{1-t+2t^2} \,  dt \)

  2. Find the derivative \( g'(x)\) of the function.   solution

    3. (a)  \(\displaystyle{ g(x)=\int_1^x \sqrt{3t^2+t^4} \, dt }\)   (b)   \(\displaystyle{ g(x)=\int_x^2 \frac{5-\sin t }{\cos t +2t}\, dt }\)     (c)   \( \displaystyle{g(x)=\int_1^{2x} (2-5t+7t^2 ) \, dt} \)   (d)  \( \displaystyle{g(x)=\int_{e^x}^{0} 5 \cos^3(t) \, dt} \)

  3. Consider the following graph of \(y=f(t)\) for the following (a)-(e).  solution

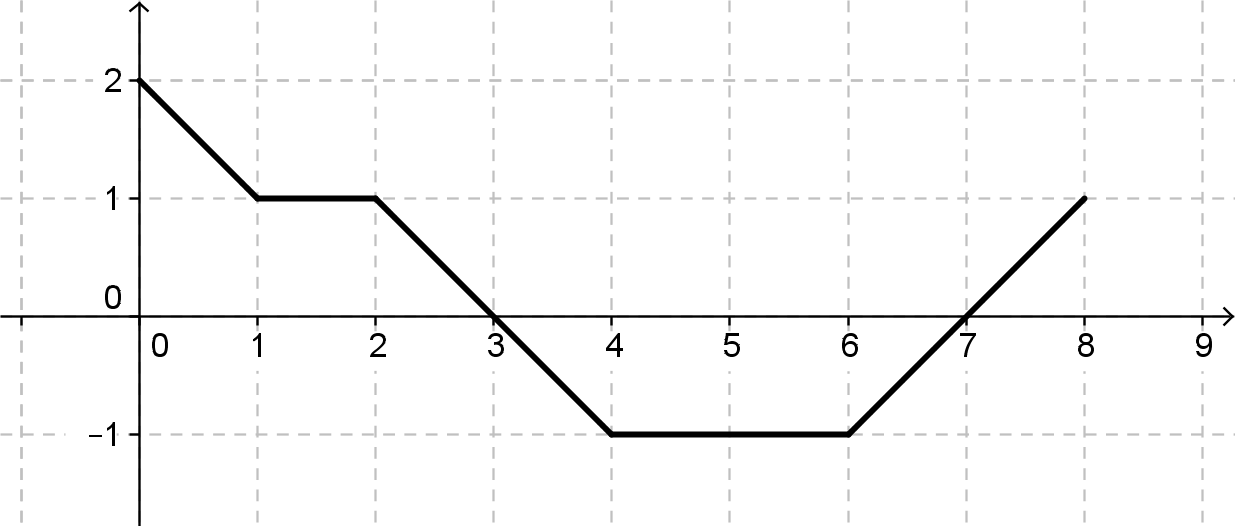
    4. pictwo 

    Evaluate (a) \(\displaystyle{\int_0^3 f(t)\, dt}\)   (b) \(\displaystyle{\int_3^7 f(t)\, dt}\)   (c) \(\displaystyle{\int_6^8 f(t)\, dt}\)  (d)\(\displaystyle{\int_0^8 f(t)\,dt}\)

    (e) Let \( \displaystyle{g(x)=\int_0^x f(t) \, dt}, \) where \(f\) is the function whose graph is shown above.    (i) What is \(g(2)\)?    (ii) At what value of \(x\) does \(g(x)\) have a local maximum?    (iii) On what intervals is \(g(x)\) increasing? Explain.


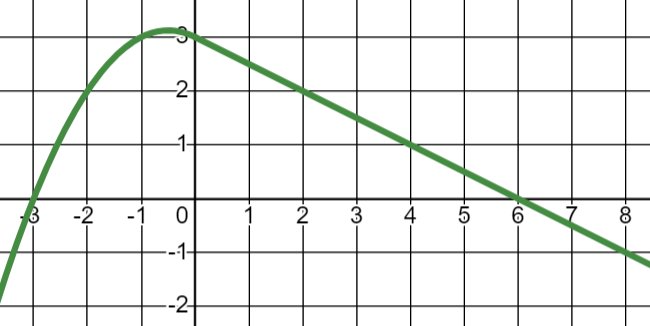
  4. Consider the following graph \(y=f(t)\). Let \( \displaystyle{g(x)=\int_0^x f(t) \, dt} \)  and   \( \displaystyle{h(x)=\int_{-2}^x f'(t) \, dt} \)   for \(x \geq -3\). (a) Find the critical numbers of \(g(x)\) on the interval \(0 \leq x \leq 8\). Justify your answer.   (b) Evaluate \(h(6), \, h'(6)\) and \(h''(6)\).   solution

    5. newpic


  5. Evaluate each integral.  solution

    6. (a) \(\displaystyle{ \int (1 + 2x + e^x) \, dx}\)    (b) \(\displaystyle{\int \frac{x-1}{\sqrt x} \, dx}\)    (c) \(\displaystyle{ \int (x^7-5x^2+2x-3) \, dx }\)   (d) \(\displaystyle{\int \frac{1+x+x^2}{x} dx}\)

    Evaluate the following definite integrals.

  6. (a) \(\displaystyle{ \int_0^1  (1+x^9+x^{99})\: dx}\)    (b) \(\displaystyle{ \int_0^2  (3x^2-1)\: dx}\)   (c) \(\displaystyle{ \int_1^8 \sqrt[3]{x}\: dx}\)   solution


  7. (a) \(\displaystyle{\int_{\ln 2}^{\ln 7}  e^{x} \:dx}\)   (b) \(\displaystyle{ \int_0^{\ln 5} (e^x-1) \: dx}\)    (c) \(\displaystyle{ \int_{-1}^0 (2x-e^x+1) \: dx} \)    solution


  8. (a) \(\displaystyle{ \int_{\pi/4}^{\pi} \, \sin (\theta)\, d\theta}\)         (b) \(\displaystyle{ \int_0^{\pi/4}\, 8 \sec^2 (\theta) \, d\theta}\)       (c) \(\displaystyle{ \int_{\pi/6}^{\pi/3}\, 8 \csc (t) \cot (t) \, dt}\)   solution


  9. (a) \(\displaystyle{ \int_0^2  (3x^2-1) \, dx}\)    (b) \(\displaystyle{ \int_{-1}^0 (2x-e^x+1) \, dx} \)    (c) \(\displaystyle{ \int_0^{\pi/4}\frac{1+\cos^2\theta}{\cos^2\theta}  \, d\theta} \)   solution


  10. (a) \(\displaystyle{ \int_0^1 \frac{2}{1+ t^2} \,  dt}\)              (b) \(\displaystyle{ \int_0^9 \sqrt{2x} \, dx} \)      solution


  11. (a) \( \displaystyle{\int_ 1^{64} \frac{1+\sqrt[3]x}{\sqrt{x}} \, dx }\)                (b) \(\displaystyle{ \int_1^9 \frac{x-1}{\sqrt{x}}  \, dx}\)       solution


  12. (a) \(\displaystyle{ \int_1^{e^2}  \frac{5}{x} \,  dx}\)             (b) \(\displaystyle{ \int_0^{\ln 5} (e^x-1) \, dx}\)    solution


  13. (a) \(\displaystyle{ \int_{-3}^1 e^{v+5} \, dv} \)          (b) \(\displaystyle{ \int_{0}^2 (6x-3)(8x^2+3) \, dx} \)    solution


  14. The velocity function for a particle moving along a line is given by \( v(t)=2t-6\) meters per second on the time interval \( 1\leq t \leq 4\). (a) Find the displacement and (b) the distance traveled by the particle during the given time interval.   solution

 


 

Back to homepage