The Definite Integral part One

  1. The graph of \(f\) is shown. Evaluate each integral by interpreting it in terms of areas.   solution

    2. (a) \( \displaystyle{\int_{0}^4 f(x)   dx}\)            (b) \( \displaystyle{\int_{6}^{10} f(x)   dx}\)           (c) \( \displaystyle{\int_{0}^{10} f(x)   dx}\)

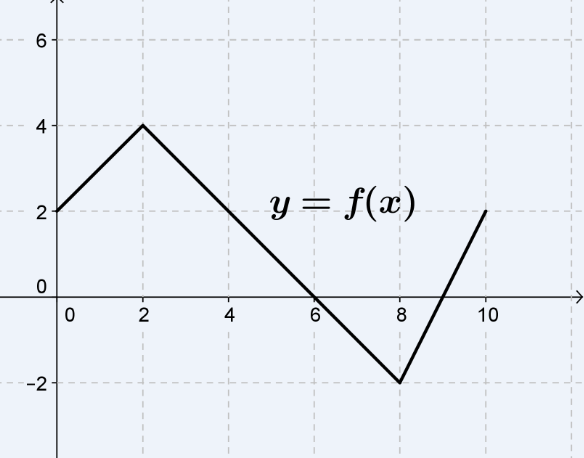
    pic one 

  2. The graph of \(g\) consists of two straight lines and a semicircle. Use it to evaluate each integral.  solution

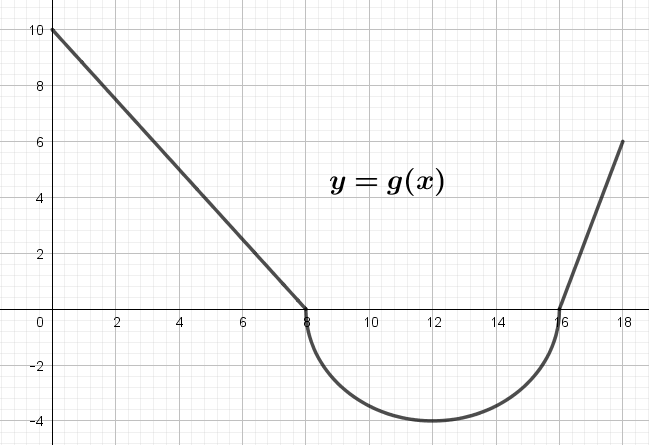
    3. (a) \( \displaystyle{\int_{0}^4 g(x) \, dx}\)   (b) \( \displaystyle{\int_{0}^{8} g(x) \, dx}\)   (c) \( \displaystyle{\int_{8}^{16} g(x) \, dx}\)    (d) \( \displaystyle{\int_{0}^{18} g(x) \, dx}\)

     

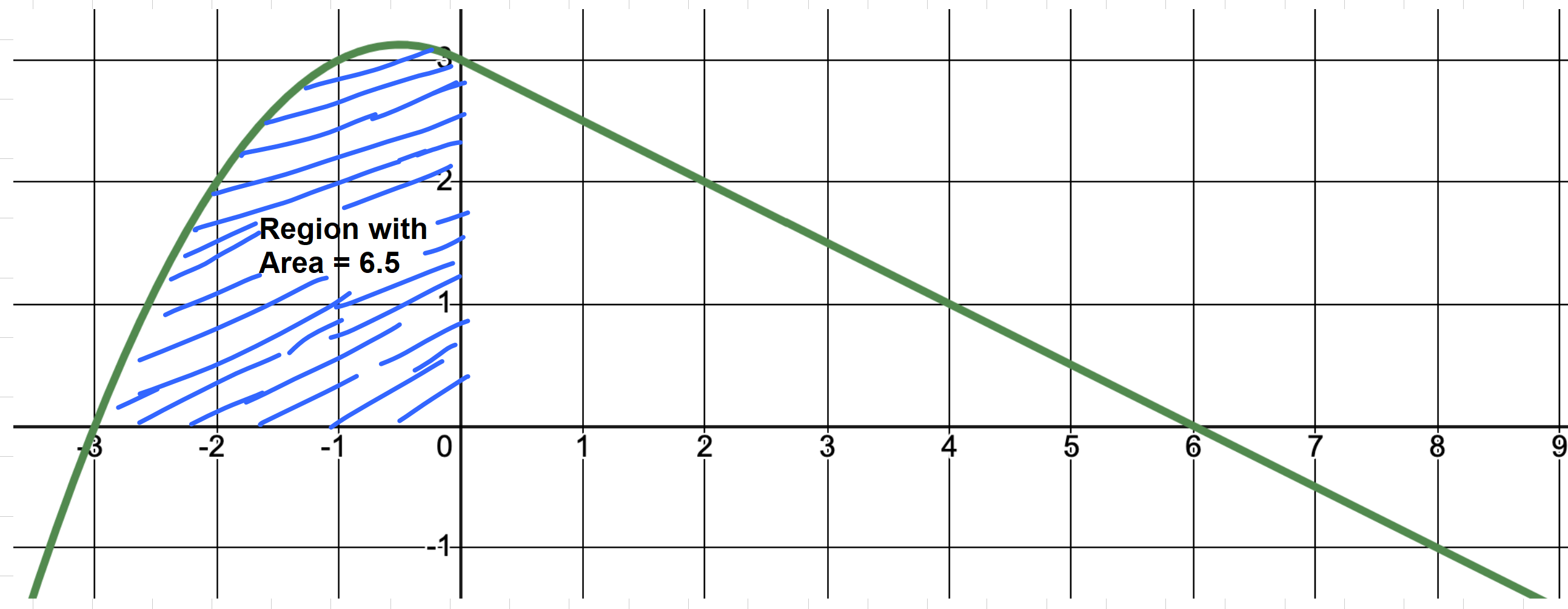
  3. Consider the following graph of a function \(y=f(x)\) which is a curve for \(x\le 0\) and a line for \(x\ge 0\). Given that the area of the left region is 6.5 as shown, evaluate (a) \( \displaystyle{\int_{0}^{-3} f(x) \, dx}\)   (b) \( \displaystyle{\int_{0}^{4} f(x) \, dx}\)    (c) \( \displaystyle{\int_{0}^{8} f(x) \, dx}\)

    4. pic   solution

  4. Evaluate each of the following integrals by interpreting it in terms of areas.   solution

    5. (a) \( \displaystyle{\int_{-2}^3 |x| \, dx}\)                  (b) \( \displaystyle{\int_{-1}^4 (4-2x)\, dx}\) 

     

  5. Evaluate each of  the following integrals by interpreting it in terms of areas.  solution

    6.  (a) \( \displaystyle{\int_{0}^6 |x-4| \, dx}\)    (b) \( \displaystyle{\int_{-2}^2 \sqrt{4-x^2} \, dx}\) 


  6. Evaluate each integral by interpreting it in terms of areas.  solution

    7. (a) \(\displaystyle  \int_{-2}^1 |x|\, dx \)     (b) \(\displaystyle \int_{1}^4 |x-2|\, dx \)      (c) \(\displaystyle   \int_{-2}^2\sqrt{4-t^2} \, dt \)


  7. If \( \displaystyle \int_0^5 f(x)\, dx = 6\) and \(\displaystyle \int_3^5 f(x)\, dx=2\), find \(\displaystyle \int_0^3 f(x)\, dx\).   solution


  8. If \( \displaystyle \int_1^6 f(x)\, dx = 7,   \int_1^6 g(x)\, dx= -2\) , find (a) \(\displaystyle \int_1^6 [3f(x)-2g(x)]\, dx\),  (b) \(\displaystyle \int_1^6 [3+f(x)]\, dx\).  solution

 

 

Back to homepage