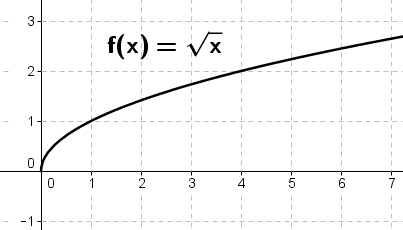Riemann Sum
1. Find an approximation of the area of the region R under the graph of the
function \(f\) on the interval \([−1, 2]\). Use \(n = 6\) subintervals. Choose the
representative points to be the left endpoints of the subintervals. \(\displaystyle{f(x) = 9 - x^2} \) solution
2. Find an approximation of the area of the region R under the graph of the
function \(f\) on the interval \([1, 3]\). Use \(n = 4\) subintervals. Choose
the representative points to be the right endpoints of the subintervals. \(f(x)=\frac{2}{x}\) solution
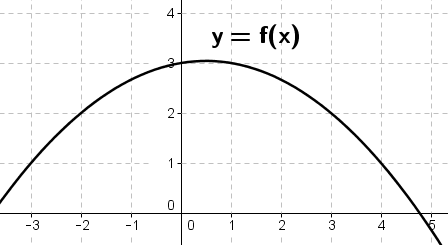
3. Divide the interval \( [-2,3]\) into five subintervals of equal length. Then approximate the area under the curve \(y=f(x)\) on \( [-2,3]\)
sketching the corresponding rectangles using left endpoints of each subinterval. Repeat this using right end points of each subinterval.
solution
4. Divide the interval \( [0,4]\) into four subintervals of equal length.
Then approximate the area under the curve \(f(x)=\sqrt{x}\) on \( [0, 4]\)
sketching the corresponding rectangles using right-end points.
solution