1. Sketch the graph of an example of a function that satisfies all  of the given conditions.

        \(\displaystyle \lim_{x \rightarrow -3} f(x)= - \infty \), \(\displaystyle \lim_{x \rightarrow 4^+} f(x)=  \infty \), \(\displaystyle \lim_{x \rightarrow 4^-} f(x)= - \infty \)

       \(\displaystyle \lim_{x \rightarrow -\infty} f(x)= 1 \), \(\displaystyle \lim_{x \rightarrow \infty} f(x)= - 2 \).



Solution



2. For the function whose graph is given below state the following.

           (a) \(\displaystyle \lim_{x \rightarrow \infty} f(x) \),         (b) \(\displaystyle \lim_{x \rightarrow -\infty} f(x) \),

           (c) \(\displaystyle \lim_{x \rightarrow 2} f(x) \),                (d) \(\displaystyle \lim_{x \rightarrow -2} f(x) \),

           (e) The equations of the asymptotes.




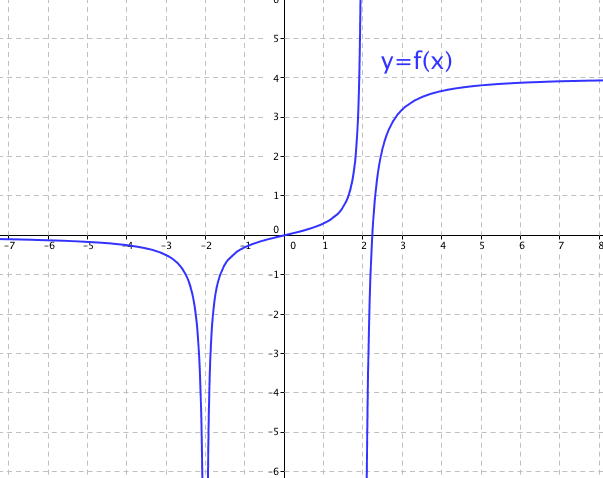
Solution


Find the limit or show that it does not exist.

3. \(\displaystyle  \lim_{x \rightarrow \infty}\frac{5x-7}{3x+4} \)


Solution


4. \(\displaystyle  \lim_{x \rightarrow \infty}\frac{5+4x^2+7x^3}{x^5-2x+4} \)


Solution


5. \(\displaystyle  \lim_{u \rightarrow \infty}\frac{u^2\sqrt{u}-u}{3u^{5/2}+5u^{3/2}-4} \)


Solution



6. \(\displaystyle  \lim_{t \rightarrow \infty}\frac{\sqrt{25t^8-16t^4+t^2}}{3t^4+4t^3-2} \)


Solution


7. \(\displaystyle  \lim_{x \rightarrow \infty}\frac{3e^x+4}{2-2e^x} \)


Solution



8. \(\displaystyle  \lim_{x \rightarrow \infty}\frac{(3x^2-1)(5x+3)^2}{(3x^2+2x+4)^2} \)


Solution