It is vital that you understand inequalities in order to do statistics. You will often be asked to decide if a value is less than .05 or greater than .05. If you can't do so, you're in BIG trouble!
Imagine a number line. Better yet, look at the one illustrated below.
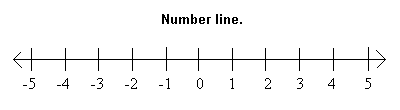
Along a standard number line, any number to the right of another number is greater than that number, indicated by the > sign. E.g., 5 is to the right of 4; therefore, 5>4. Any number to the left of another number on the line is less than that number, indicated by the < sign. -1 is to the left of 0; therefore, -1<0.
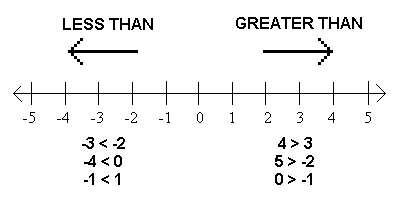
Particularly critical are numbers close to zero. The following number line illustrates the numbers between -1 and +1. On each side of zero, the numbers are shown on a log scale. I.e., on the negative side, each tick mark represents a value that is one-tenth of the value to its left. On the positive side, each tick mark represents a value ten times the value to its left.
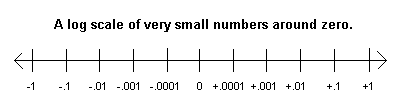
It is important that you understand this scale, especially on the positive side of zero. Notice that .0001 is closer to zero than .001, which is closer to zero than .01, which is closer to zero than .1. Notice also that .0001 is to the left of .001 and, therefore, .0001<.001, and so on.
If it upsets you to be told something so trivial that you learned back in the 8th grade, then good for you! But a lot of students who have come through this class in the past couldn't do this.
Here is an ordered sequence of numbers around .05. All the numbers to the left of .05 are less than .05, and all the numbers to the right are greater than .05. If you don't understand why, you've got problems!
0 .001 .003 .013 .025 .033 .049 .0499 .05 .0501 .051 .077 .080 .122 .333 .488 .678
You should be able to look at a small positive number between 0 and 1 and decide in an instant if it is less than or greater than .05. Without that skill, you're sunk!
Here's another test for you: 4.89E-04. Is this number less than or greater than .05. If you said greater than, go directly to arithmetic jail. Do not pass GO. Do not collect a passing grade in statistics!